时间复杂度

常数时间操作O(1)

  • 操作时间是固定的次数，跟数据量本身没有关系，就是其时间复杂度是O(1),比如总是比较1次或者3次，比如总是累加3次，总是赋值3次等等，无论样本数据量是多少，总是如此，我们就说起操作时间是常数时间，也就是O(1)

  • 实际评估过程中一般是循环多多少次，比较了多少次等等计算出一个表达式，然后对于表达式只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分 如果记为f(N)，那么时间复杂度为O(f(N)). N为样本量

  • 一个简单的例子：

    比如计算出的表达式为f(N)=2$N^2$+3N+3 这里面的高阶项就是$N^2$，对应高阶项的系数就是2 低阶项就是3N和3 最后f(N)=$N^2$

  • 算法流程的好坏，先看时间复杂度的指标，然后再分 析不同数据样本下的实际运行时间，也就是常数项时间

例子

  • 一个有序数组A，另一个无序数组B，请打印B中的所有不在A中的数，A数 组长度为N，B数组长度为M。

    算法流程1:对于数组B中的每一个数，都在A中通过遍历的方式找一下;

    算法流程2:对于数组B中的每一个数，都在A中通过二分的方式找一下;

    算法流程3:先把数组B排序，然后用类似外排的方式打印所有在A中出现 的数;

代码实现及算法时间复杂度分析

三种算法代码实现 二分有递归和非递归 排序用的是归并递归实现 ```c++ // 一个**有序**数组A，另一个**无序**数组B，请打印B中的所有不在A中的数，A数 组长度为N，B数组长度为M。 // 算法流程1:对于数组B中的每一个数，都在A中通过遍历的方式找一下; // 算法流程2:对于数组B中的每一个数，都在A中通过二分的方式找一下; // 算法流程3:先把数组B排序，然后用类似外排的方式打印所有在A中出现 的数; #include using namespace std; //打印数组 void printArray(int a[],int la){ cout<<"["; for(int i=0;i>1 ); if (toFindmid-1区间查找 isIn=binarySearchIsInARecur(A,l,mid-1,toFind); }else if (toFind>A[mid]) { //如果大于A[mid] 那么就去A数组中 mid+1--->r 区间查找 isIn=binarySearchIsInARecur(A,mid+1,r,toFind); }else{ return true;//等于A[mid]直接返回true } return isIn; } //二分查找toFind元素是否在A数组中 非递归版本 bool binarySearchIsInA(int A[],int l,int r,int toFind){ //这里简单期间没做边界检查 while ( l <= r){ int mid=l + ( (r-l)>>1 ); if (toFindmid-1区间查找 r=mid-1; }else if ( toFind>A[mid]){//如果大于A[mid] 那么就去A数组中 mid+1-->r 区间查找 l=mid+1; }else{ return true; } } return false; } void printBNotInA1(int A[],int B[],int lenA,int lenB){ //暴力搜索 这里简单期间没做边界检查 for (int i=0;imid mid+1--->r 2个排好序的分片合并 void merge2Slice(int a[],int l,int mid,int r){ int *help= new int[r-l+1];//声明1个辅助数组 合并后先放入help数组 然后在copy回原数组 int l1=l,r1=mid,l2=mid+1,r2=r;//便于理解 分割成为2个区间 l1--r1 l2--r2 int cur1=l1,cur2=l2,hIndex=0;//刚开始下标分别指向2个区间的开始位置 辅助数组的下标刚开始赋值为0 while (cur1<=r1 && cur2<=r2 ){//任意1个区间遍历完成退出循环 if (a[cur1]>1 ); mergeSortRecur(A,l,mid);//左半边归并排序 mergeSortRecur(A,mid+1,r);//右半边归并排序 merge2Slice(A,l,mid,r);//将2个分片合并 } void printBNotInA3(int A[],int B[],int lenA,int lenB){ //先用归并排序实现B数组的排序 再用外排的思想快速判断是否在A中 mergeSortRecur(B,0,lenB-1);//先归并排序 //外排 int curA=0,curB=0;//分别指向数组的第一个元素 while ( curB<=(lenB-1) && curA<=(lenA-1)){ if ( B[curB]

算法1

  • 2层循环遍历 O(M*N)

算法2

  • 也是2层循环 只不过第二层循环用二分查找 所以二分的复杂度为logN 总体为O(M*logN)

算法3

  • B归并排序 O(MlogM) 外排O(M+N) 总体为O(MlogM)+O(M+N)

算法1肯定是最差 算法2、3要看AB数组的样本量差距才能决定

Master公式计算递归时间复杂度

递归求数组中的最大值

#include<iostream>
using namespace std;
//master公式求解常见递归的时间复杂度
//求一个数组的最大值 递归实现 l为最小下标 r为最大下标
int getMax(int A[],int l,int r){
    //base case 如果l==r 只有一个元素 直接返回该元素即可
    if(l==r) return A[l];
    int mid=l + ( (r-l)>>1 );
    int maxL=getMax(A,l,mid);//得到左边的区间的最大值
    int maxR=getMax(A,mid+1,r);//得到右边区间的最大值
    return maxL>maxR?maxL:maxR;
}
int main(){
    int A[]={8,7,0,6,2,4,-1};
    cout<<"max in A="<<getMax(A,0,6)<<endl;
}

master公式T(N) = a*T(N/b) + O(N^d)

  1. log(b,a) > d -> 复杂度为O(N^log(b,a))

  2. log(b,a) = d -> 复杂度为O(N^d * logN)

  3. log(b,a) < d -> 复杂度为O(N^d)

N为样本量 b为每次把样本量分成多少分 在这里每次都分成2份 b=2

a为递归函数在逻辑代码中调用了几次，在本例中得到左边右边区间的最大值分别发生一次 总共为2次

递归完成后的处理对应的时间复杂度为N的d次方，在这里递归完成后也就比较了一下maxL和maxR 返回器最大值 所以时间复杂为常数也就是N的d次方为1 所以d为0

满足master公式1条件 所以时间复杂度为 N^log(2,2)=N 也就是O(N)

冒泡排序

介绍

冒泡排序是一种比较简单的排序，之所以叫冒泡，是因为在两两比较的过程中较大的数就像冒泡一样被换到后面。详细解释：依次比较相邻的两个数，前面的数大于后面的数，则交换，将较大的数挪动到后面
  • 第1轮: 比较1 – N 经过依次相邻两两比较交换 最大的数则放到了最后
  • 第2轮: 比较1 –N-1 经过依次相邻两两比较交换 第2大的数则放到了N-1的位置
  • 第N-1轮:比较1 – 2 前2个数两两比较交换 整个过程完成

代码

BubbleSort ```go func BubbleSort(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } //外层循环控控制每轮循环两两比较的最大下标 第1次为N-1 最后一次为1(也就是最前面的2个元素) for endPos := len(a) - 1; endPos > 0; endPos-- { //内层循环完成两两比较交换 for i := 0; i < endPos; i++ { if a[i] > a[i+1] { a[i], a[i+1] = a[i+1], a[i] } } } } ```

时间复杂度

O($N^2$)

稳定性

**稳定** 因为如果2个数相等 则他们的相对位置 并没有发生改变

优化

看内层循环 如果并没有发生数据交换 则证明所有数据已经排序完成，这个时候直接结束即可 加一个标志判断即可
BubbleSortOpt ```go func BubbleSort(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } isChg := false //外层循环控控制每轮循环两两比较的最大下标 第1次为N-1 最后一次为1(也就是最前面的2个元素) for endPos := len(a) - 1; endPos > 0; endPos-- { //内层循环完成两两比较交换 for i := 0; i < endPos; i++ { if a[i] > a[i+1] { a[i], a[i+1] = a[i+1], a[i] isChg = true } } if !isChg { //如果内层循环没有发生数据交换 则表明所有数据都已经排序完成 直接退出循环即可 break } } } ```

网搜图解

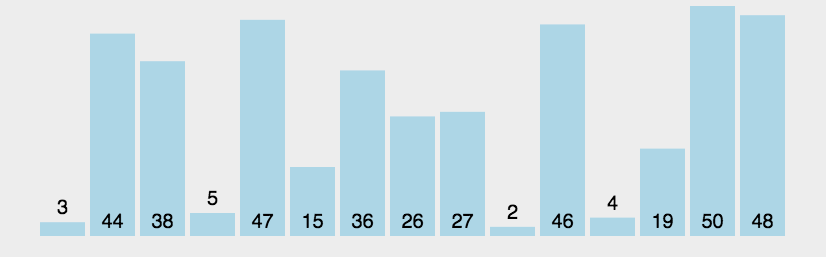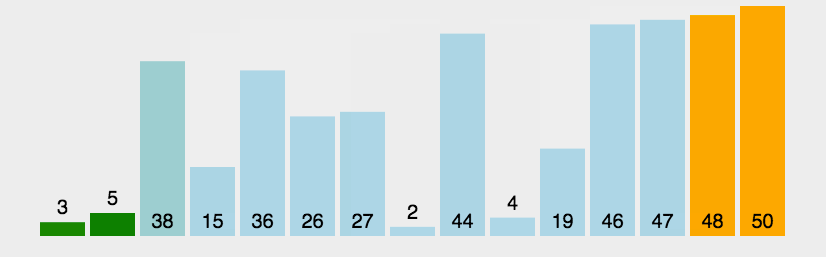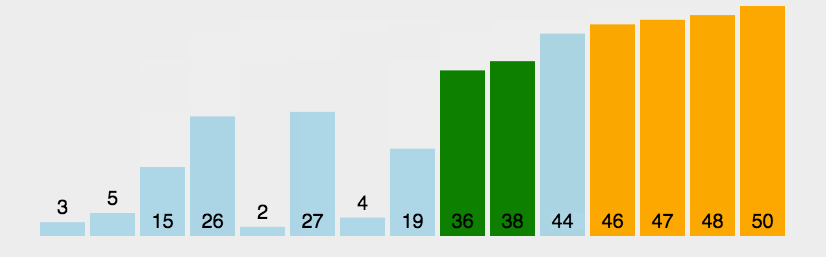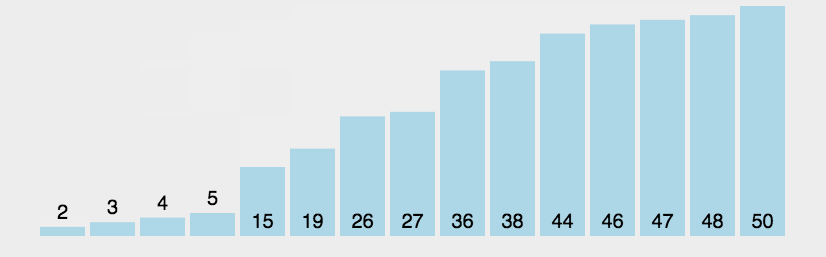
摘自: https://www.cnblogs.com/onepixel/p/7674659.html

插入排序

介绍

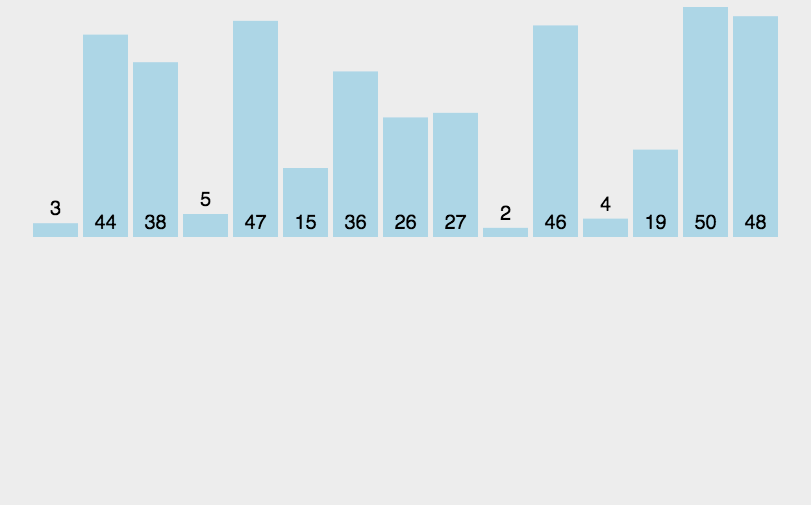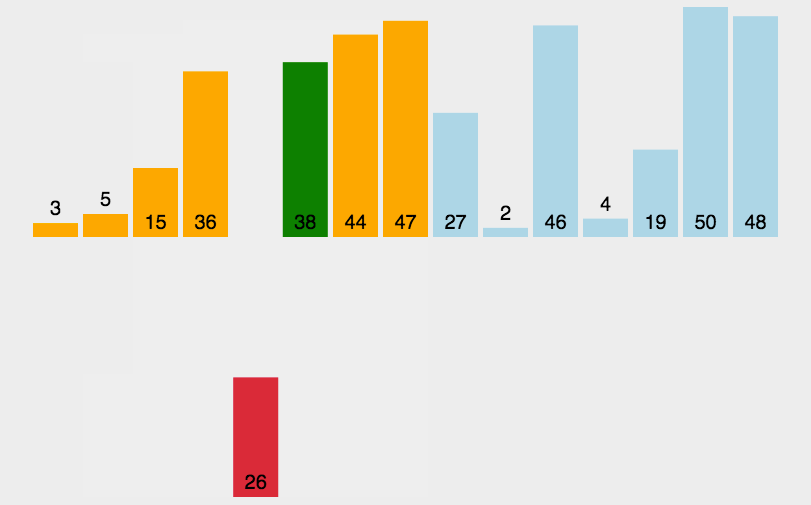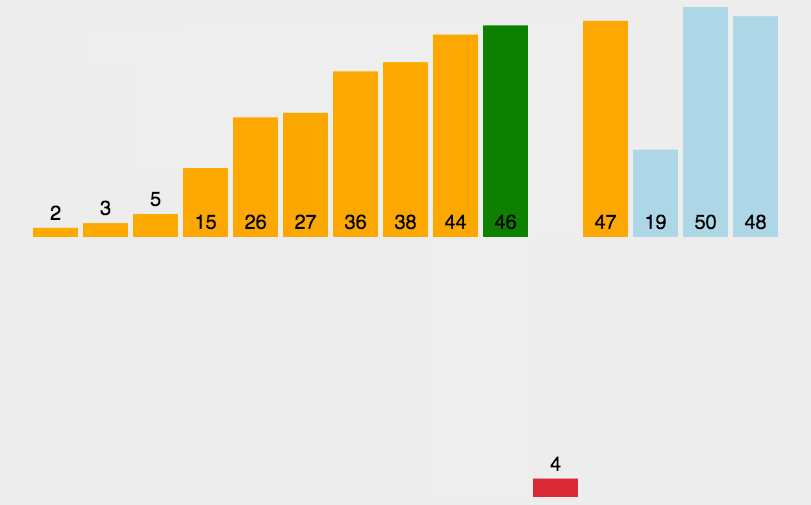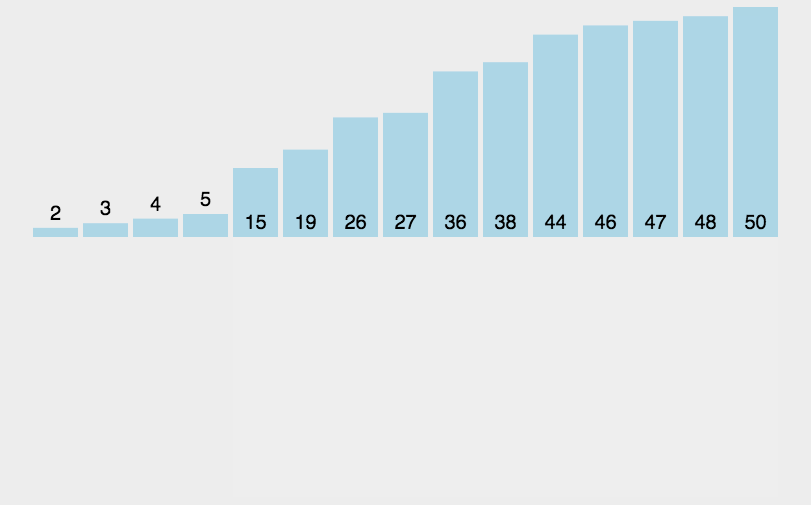
插入排序顾名思义就是将一个待排序的元素，插入到一组已经排好序的元素中，如果形象比喻下，可以想象一下打牌，拿起来第一张牌自然就是排好序的，拿起第二张则跟第一张进行比较，插入到合适的位置。接下来拿第三张 跟前面2张已经排好序的比较，插入合适的位置，依次类推，拿完所有的牌，顺序自然也排好了。

将待排序的元素分为有序区和无序区，按照顺序每次从无序区拿一个元素，插入插入到有序区，直到所有无序区的元素都插入有序区，整个排序过程结束。第一次有序区为第1个元素，无序区为第2---N个元素，拿出第2个元素插入到有序区。

代码

InsertSort ```go func InsertSort(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } //j为无序区的第一个元素 对应下标从1开始，每次后移一个位置 for j := 1; j < len(a); j++ { //内层循环完成比较插入 倒序依次跟有序区的元素进行比较，如果小于有序区的元素 则交换 for i := j; i > 0; i-- { if a[i] < a[i-1] { a[i], a[i-1] = a[i-1], a[i] } } } } ```

时间复杂度

O($N^2$)

算法稳定性

**稳定** 没有改变两个相等元素的相对位置

优化

上面代码内层循环在查找待插入位置时是倒序逐个比较的，在查找待插入位置时候是可以优化的，**采用二分查找可以有效减少比较次数**，但**优化后的插入算法则变为不稳定的**
InsertSortOpt ```go //BinSerachInsertIndex 二分查找在a数组 begin到end区间 key元素的插入位置 func BinSerachInsertIndex(a []int, begin int, end int, key int) int { pos := -1 //需要插入的位置 for begin <= end { mid := begin + (end-begin)/2 if a[mid] == key { //如果等于key 则找到位置 pos = mid + 1 break } else if a[mid] < key { begin = mid + 1 } else { end = mid - 1 } } if pos == -1 { pos = begin } return pos } func InsertSortOpt(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } for j := 1; j < len(a); j++ { begin, end, key := 0, j-1, a[j] //找到插入的位置 pos := BinSerachInsertIndex(a, begin, end, key) //将pos到end区间的元素逐个后移 for index := j; index > pos; index-- { a[index] = a[index-1] } //插入待排序元素 a[pos] = key } } ```

网搜图解

摘自:https://www.cnblogs.com/onepixel/p/7674659.html

归并排序

介绍

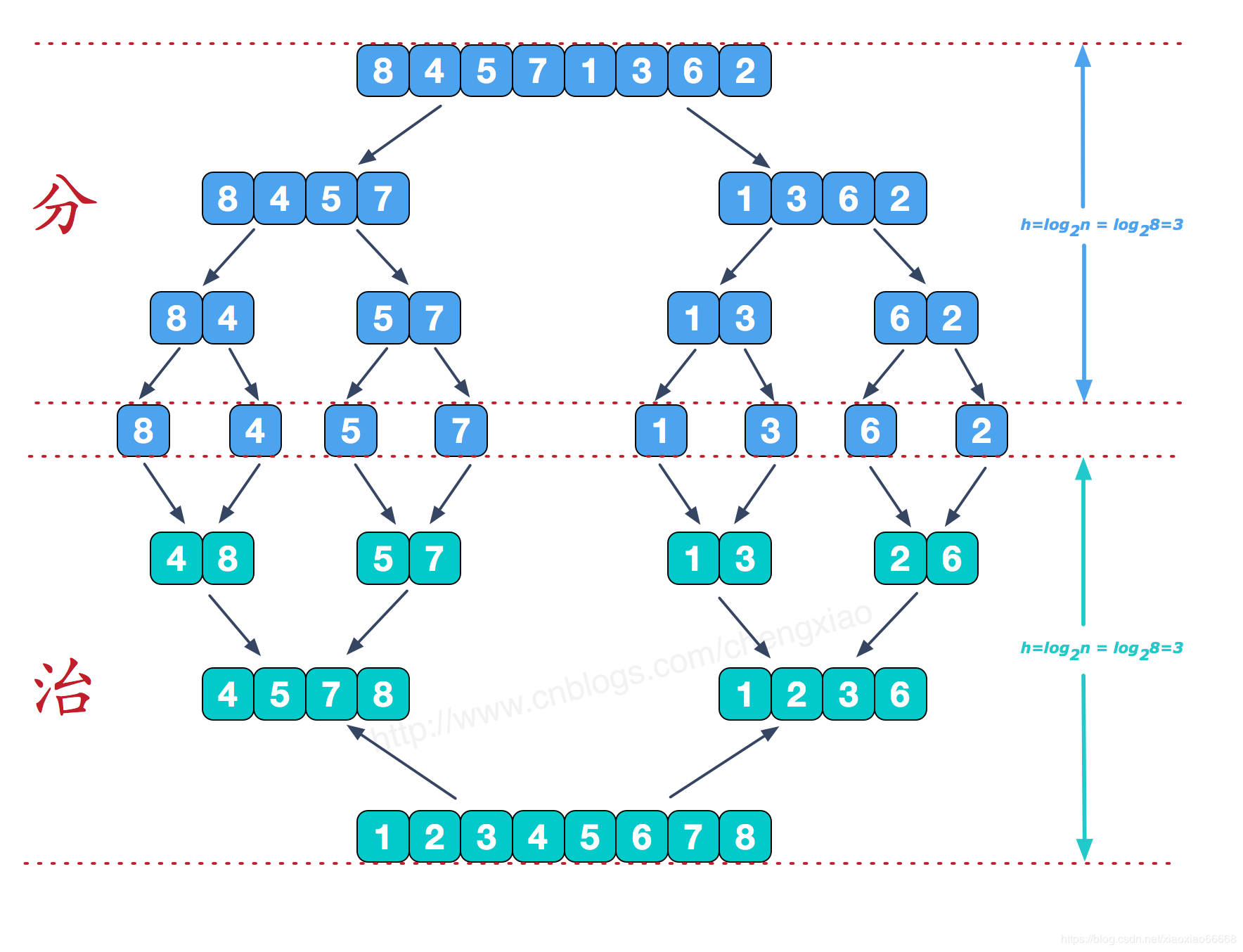
MergeSort 合并两个有序的序列为1的大的有序的序列，最典型的归并排序可以分2个大的步骤：

1 采用递归思想 将一个大的序列:二分为大致平均的子序列，然后针对每个子序列都再递归二分(最后每个子序列长度都为1)

2 两两子序列合并为有序序列 直到所有子序列合并完成

整体归并排序也用到了很重要的分治思想，也就是将大的问题分为小的问题 逐个解决

代码

MergeSort ```go func MergeSort(a []int, left int, right int) { //校验 if len(a) < 2 || left < 0 || right > len(a) || left >= right { return } mid := left + (right-left)/2 //数组中间位置 MergeSort(a, left, mid) //左边归并排序 MergeSort(a, mid+1, right) //右边递归排序 MergeSlice(a, left, mid, right) //合并2个子序列为大的有序序列 } func MergeSlice(a []int, left int, mid int, right int) { //先生成1个辅助空间 长度 容量都是right-left+1 help := make([]int, right-left+1, right-left+1) helpIndex := 0 //help数组起始位置 填入一个数值 往后移动一位 //定义2个下标 开始分别指向2个子区间的最开始位置 然后逐个遍历 LIndex := left RIndex := mid + 1 for LIndex <= mid && RIndex <= right { if a[LIndex] <= a[RIndex] { //左边区间数值较小 左边进辅助空间 help[helpIndex] = a[LIndex] LIndex++ } else { help[helpIndex] = a[RIndex] RIndex++ } helpIndex++ //不管左边区间进辅助还是右边区间 辅助数组下标下移一个位置 因为必定进了一个数 } for LIndex <= mid { //如果遍历完成 左边区间还有数没放进辅助数组 那就说明剩下的左边区间数较大 依次cp进辅助 help[helpIndex] = a[LIndex] LIndex++ helpIndex++ } for RIndex <= right { //如果遍历完成 左边区间还有数没放进辅助数组 那就说明剩下的左边区间数较大 依次cp进辅助 help[helpIndex] = a[RIndex] RIndex++ helpIndex++ } //辅助空间已经排好序 覆盖填回原数组 for i := 0; i < helpIndex; i++ { a[left+i] = help[i] } } ```

时间复杂度

O( NLogN)

算法稳定性

稳定 需要merge合并的时候 左边区域<=右边区域的时候 先copy左边

优化

规模较小的时候 不用归并，改为插排

递归其实非常消耗性能 规模较小的时候可以不再递归 较少递归调用次数
MergeSortOpt ```go func MergeSortOpt(a []int, left int, right int) { //一个数 为空 下标不合法 拆分完成 if len(a) < 2 || left < 0 || right > len(a) || left >= right { return } if left+20 >= right {//这里增加几行代码 规模较小 改为插排 InsertSort(a[left : right+1]) return } mid := left + (right-left)/2 //数组中间位置 MergeSort(a, left, mid) //左边归并排序 MergeSort(a, mid+1, right) //右边递归排序 MergeSlice(a, left, mid, right) //合并2个子序列为大的有序序列 } ```

检查合并前两个数组是否已经有序 没有必要再调用合并了

MergeSortOpt2 ```go func MergeSortOpt2(a []int, left int, right int) { //一个数 为空 下标不合法 拆分完成 if len(a) < 2 || left < 0 || right > len(a) || left >= right { return } if left+20 >= right {//这里增加几行代码 规模较小 改为插排 InsertSort(a[left : right+1]) return } mid := left + (right-left)/2 //数组中间位置 MergeSort(a, left, mid) //左边归并排序 MergeSort(a, mid+1, right) //右边递归排序 if a[mid]<=a[mid+1]{//如果2个子序列本身已经有序 无需再合并 return } MergeSlice(a, left, mid, right) //合并2个子序列为大的有序序列 } ```

网搜图解

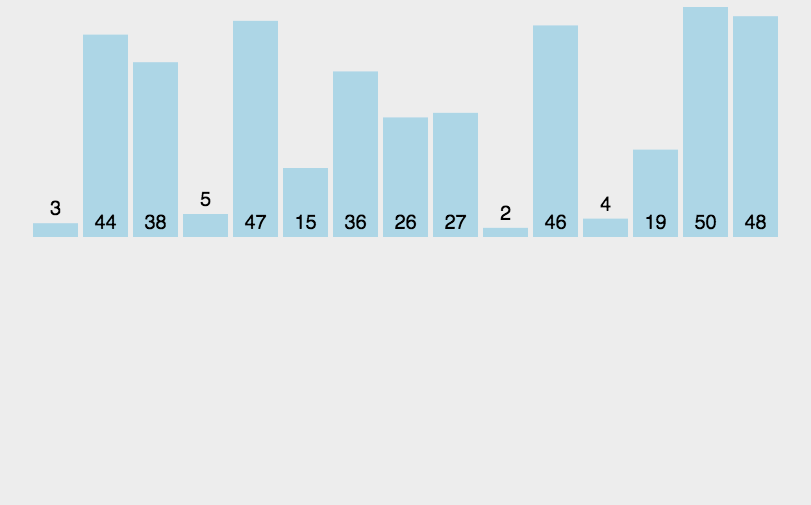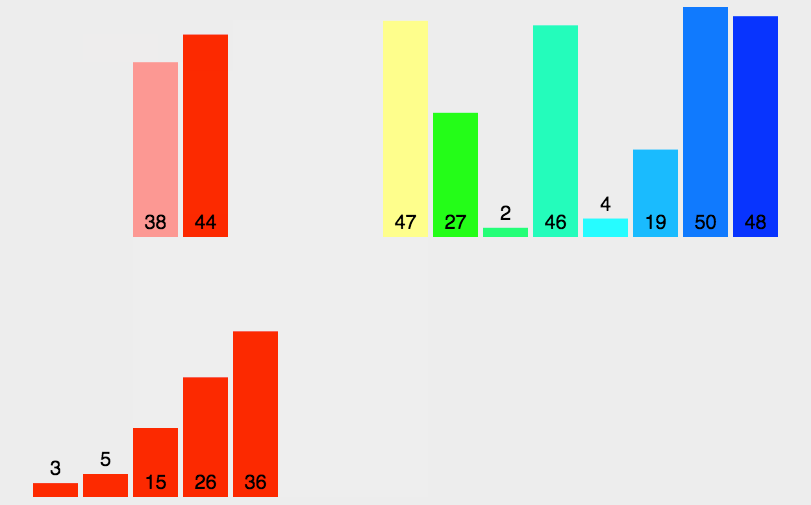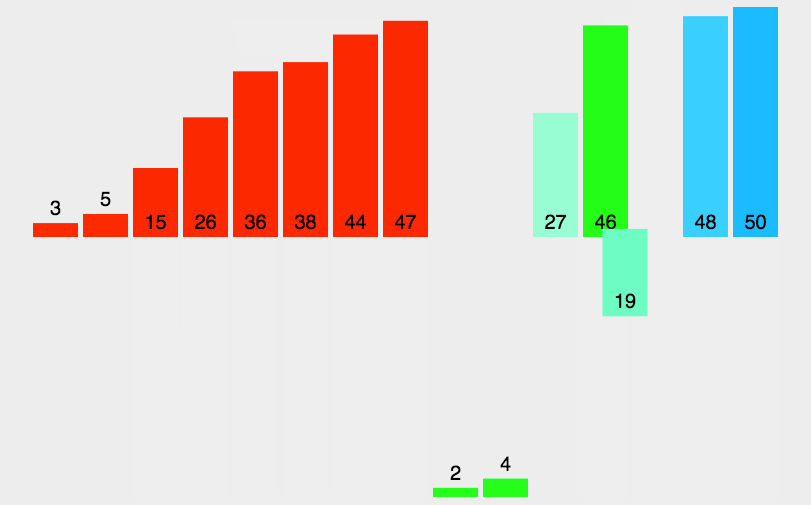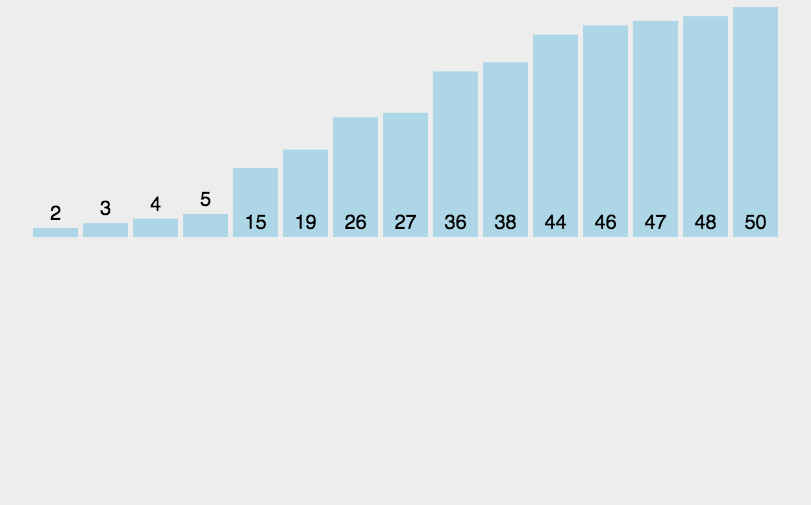
选择排序

介绍

每轮都选择一个极值(最大或者最小)放到数组的某一端，其实也是分为有序区和无序区，刚开始全是无序区，

第1轮 遍历N个数 挑选极值放到数组最左侧 有序区有1个数

第2轮 遍历剩下的N-1个数，挑选极值放入数组第2个位置，也就是依次放入有序区

…

直到剩下最后一个元素 这个元素自然是整个数组的极值 整个数组排序完成

代码

SelectSort ```go func SelectSort(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } for j := 0; j < len(a)-1; j++ {//控制每轮循环 遍历比较的元素个数 min := j //min记录最小元素下标 for i := j + 1; i < len(a); i++ { if a[min] > a[i] { min = i } } a[j], a[min] = a[min], a[j] //将最小元素依次放入有序区 } } ```

时间复杂度

O($N^2$)

算法稳定性

不稳定 会改变两个相等元素本身的相对位置  如 (7) 2 4 8 3 4 [7] 1  第一轮下来(7)会跑到最后

优化

修改内层循环，每一轮遍历 不仅找到最小下标 也要找到最大下标 最小放数组左边，最大放数组右边，减少循环次数，当然外层循环条件也要修改，最开始无序区为整个数组 每一轮下来 数组两端2个元素变为有序，有序区从两端往中间扩大，直到所有元素都为有序
SelectSortOpt ```go func SelectSortOPT(a []int) { if len(a) < 2 { //一个数或者为空 不用排序 return } //刚开始left right分别为数组最小和最大下标 每轮循环left和rignt分别放置最小和最大值 //终止条件为left==right 每轮循环后left右移 right左移 for left, right := 0, len(a)-1; left < right; left, right = left+1, right-1 { minIndex, maxIndex := left, right for i := left; i <= right; i++ { if a[i] < a[minIndex] { //找到最小值下标 minIndex = i } if a[i] > a[maxIndex] { //找到最大值下标 maxIndex = i } } a[left], a[minIndex] = a[minIndex], a[left]//最小的放当前无序区最左边 if left == maxIndex { //如最大下标就是刚开始的最小下标 因为已经交换到了minIndex位置 所以最大下标也要跟着修改 maxIndex = minIndex } a[maxIndex], a[right] = a[right], a[maxIndex]//最大值放到当前无序区最右边 } } ```

网搜图解

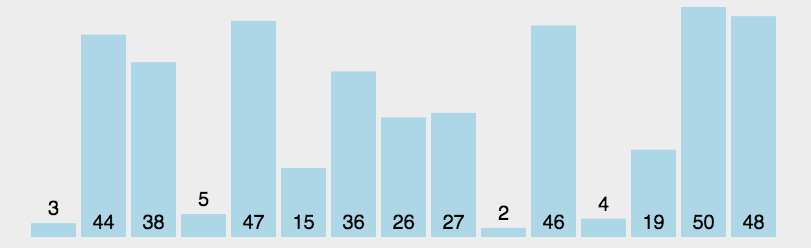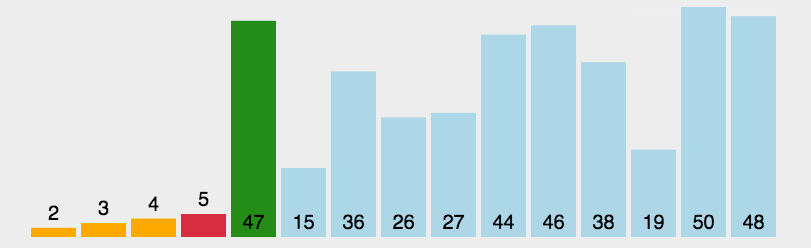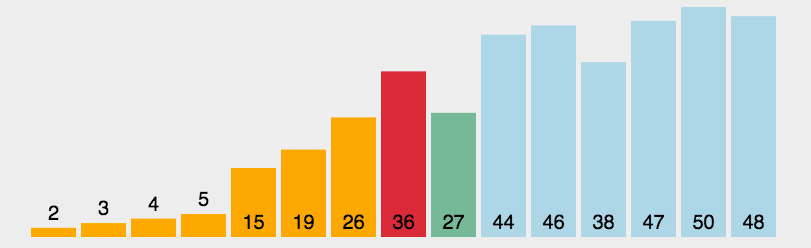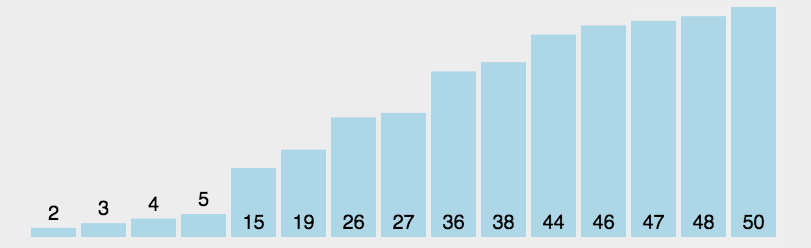
摘自： https://www.cnblogs.com/onepixel/p/7674659.html

堆排序

介绍

二叉堆介绍

堆排序是借助堆这种数据结构进行排序，又分为最大堆和最小堆。堆也分很多种，这里用二叉堆，下面从网上找到的2张图展示下最大堆和最小堆。

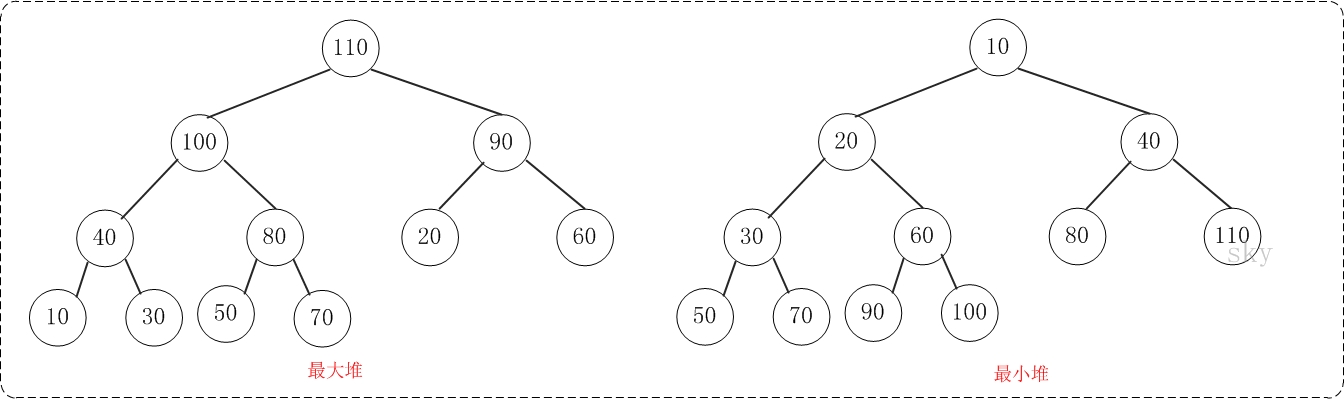
最大堆 所有父节点都**>=**两个子节点   最小堆 所有父节点都**<=**两个子节点

最大堆 可用于升序排序    最小堆可用于降序排序

二叉堆实现方式不止一种，这里选择最简单的数组实现，下图展示二叉堆如何用数组存放以及父子节点关系如何对应到数组下标关系。

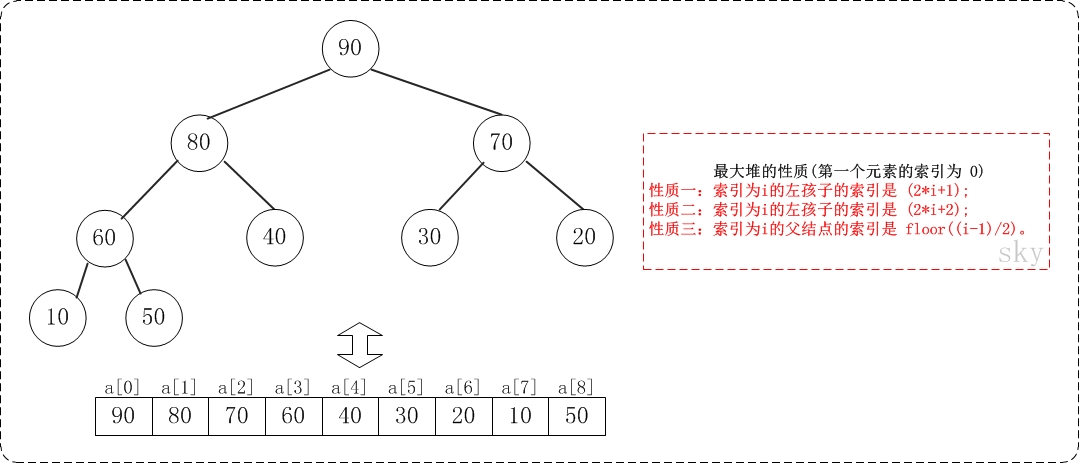
堆排序大致过程

  • 首选遍历数组 构建二叉堆(数组实现)

  • 交换堆头尾两个元素，也就是数组头尾元素，最大值放到了数组最后一个元素。因为根节点发生变化

    所以重新堆化，范围不包括最后一个元素，最后一个元素相当于已经输出排序完成，为最大值。

  • 对于重新堆化的前面N-1个元素 循环执行第2步 直到输出所有堆节点 完成最终排序

代码

最大堆

MaxHeapSort ```go func MaxHeapSort(a []int) { size:=len(a)//数组长度 if size < 2 { return } for i := 0; i < len(a); i++ {//遍历数组 构建堆 MaxHeapInsert(a, i) } for size > 0 { a[0], a[size-1] = a[size-1], a[0] //将当前堆顶也就是最大值放到最后 把最后的元素换到堆顶 然后重塑堆 size-- MaxHeapify(a, 0, size) } } func MaxHeapInsert(a []int, index int) { //如果插入节点大于父节点 则需要向上调整 先跟父节点交换 然后再比较上面的父节点 for parentIndex := (index - 1) / 2; a[index] > a[parentIndex]; index, parentIndex = parentIndex, (index-1)/2 { a[index], a[parentIndex] = a[parentIndex], a[index] } } //大堆 重新堆化过程 func MaxHeapify(a []int, index int, size int) { for maxIndex := -1; maxIndex != index; { maxIndex = index leftIndex := 2*index + 1 rightIndex := 2*index + 2 //求当前节点 左孩子 右孩子中最大值对应的下标 if leftIndex < size && a[maxIndex] < a[leftIndex] { maxIndex = leftIndex } if rightIndex < size && a[maxIndex] < a[rightIndex] { maxIndex = rightIndex } if maxIndex != index { a[index], a[maxIndex] = a[maxIndex], a[index] //跟左孩子、右孩子中最大的交换 index = maxIndex maxIndex = -1 } } } ```

最小堆

MinHeapSort ```go func MinHeapSort(a []int) { if len(a) < 2 { return } for i := 0; i < len(a); i++ { MinHeapInsert(a, i) } size := len(a) for size > 0 { a[0], a[size-1] = a[size-1], a[0] //将当前堆顶也就是最大值放到最后 把最后的元素换到堆顶 然后重塑堆 size-- MinHeapify(a, 0, size) } } //MinHeapInsert 创建大堆 数组实现 index为要插入的元素下标 //节点下标为i 对应左孩子为2*i+1 右边孩子为2*i+2 //节点下标为i 对应父节点为(i-1)/2 func MinHeapInsert(a []int, index int) { parentIndex := (index - 1) / 2 for a[index] < a[parentIndex] { //如果插入节点小于父节点 则需要向上调整 先跟父节点交换 然后再比较上面的父节点 a[index], a[parentIndex] = a[parentIndex], a[index] index = parentIndex parentIndex = (index - 1) / 2 } } //MinHeapify 下标index发生了变化 重塑堆 一路向下调整 如果两个孩子中有一个比自己小 则交换 然后继续往下调整找到比自己小的孩子 然后跟其交换 //节点下标为i 对应左孩子为2*i+1 右边孩子为2*i+2 //节点下标为i 对应父节点为(i-1)/2 func MinHeapify(a []int, index int, size int) { for minIndex := -1; minIndex != index; { minIndex = index leftIndex := 2*index + 1 rightIndex := 2*index + 2 //求当前节点 左孩子 右孩子中最小值对应的下标 if leftIndex < size && a[minIndex] > a[leftIndex] { minIndex = leftIndex } if rightIndex < size && a[minIndex] > a[rightIndex] { minIndex = rightIndex } if minIndex != index { a[index], a[minIndex] = a[minIndex], a[index] //跟左孩子、右孩子中最小的交换 index = minIndex minIndex = -1 } } } ```
## 时间复杂度 
O(NlogN)

算法稳定性

不稳定 插入的时候就有可能不稳定了

优化

当前实现的就是原地堆排序，没有使用额外的辅助空间，暂无好的优化思路，待补充

网搜图解

其它说明

​ 堆在c++和java中都有系统级的实现，可以直接使用，只不过如果是自定义的类型，需要重载比较运算符。

希尔排序

介绍

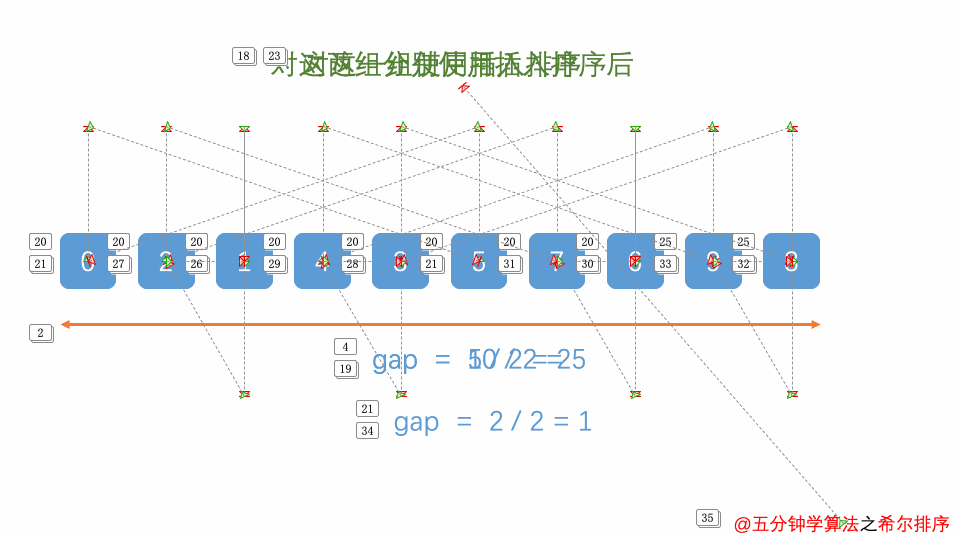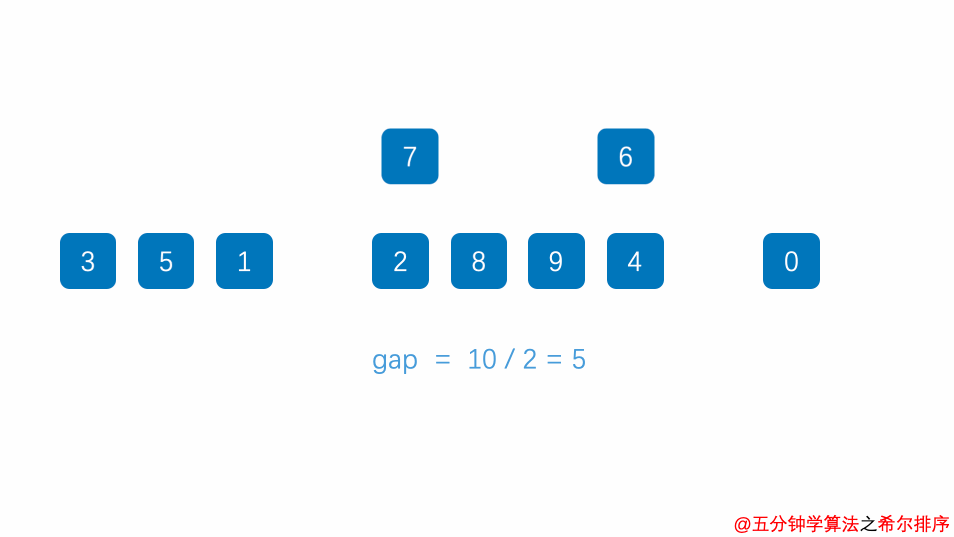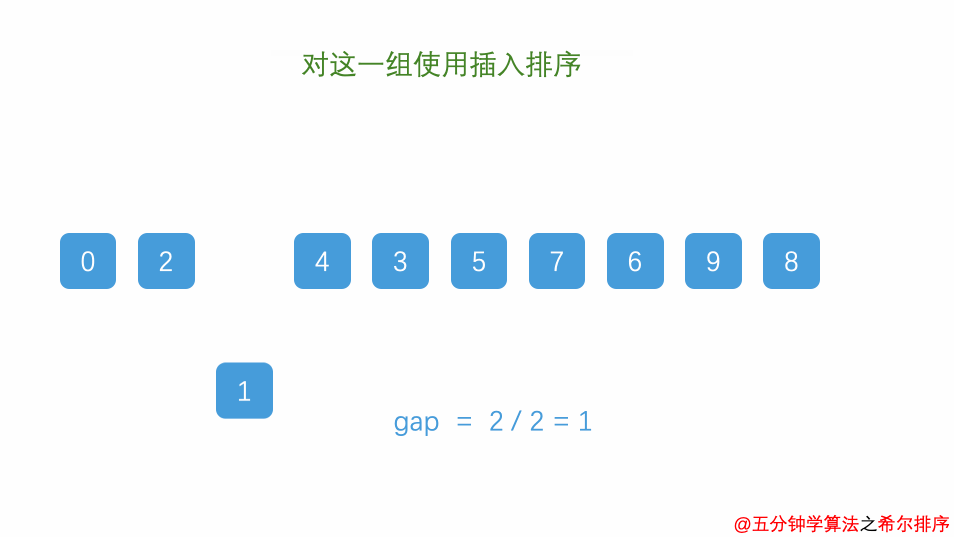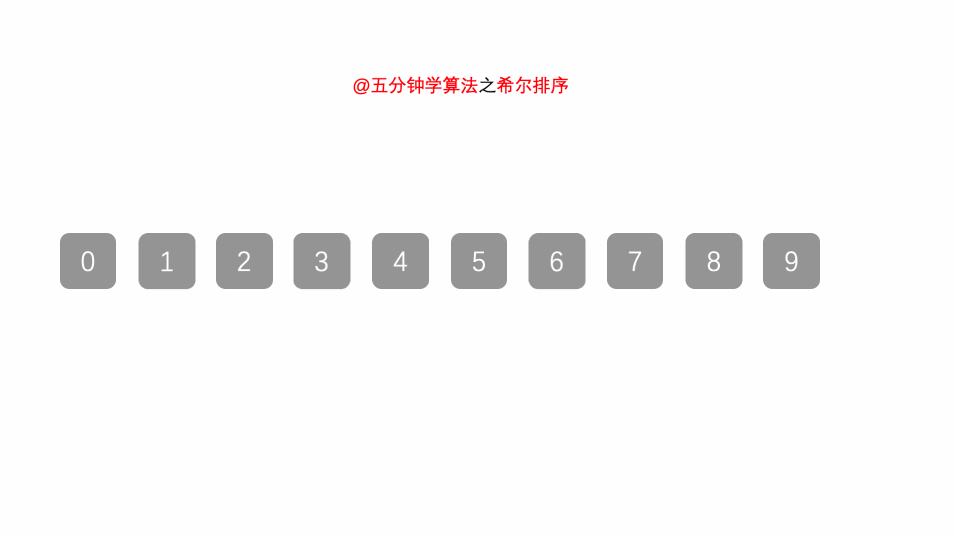
希尔排序是直接插入排序的优化版本，由一个叫shell的人提出来的，核心思想是按照步长分组，然后每组分组插排，然后缩短步长分组，继续每组插排，最后步长为1，变为直接插排。

关于步长及缩短步长如何选择，有很多种方案，可以直接分半，然后再除以2 最后为1，这里采用的Knuth序列，也就是按照下面的规律递增

gap=1—–»gap=3*gap+1

代码

ShellSort ```go func ShellSort(a []int) { //步长采用knuth序列 变化规律为 h=1 ---> h = 3*h+1 h := 1 for h <= len(a)/3 { h = 3*h + 1 } //控制gap递减 最后变为1 for gap := h; gap > 0; gap = (gap - 1) / 3 { //控制分组 for j := gap; j < len(a); j++ { //每组进行直接插排 for i := j; i > gap-1; i = i - gap { if a[i] < a[i-gap] { a[i], a[i-gap] = a[i-gap], a[i] } } } } } ```

时间复杂度

O($N^3/2$)

算法稳定性

不稳定

优化

待补充

网搜图解

快速排序

介绍

快速排序主要用到了分治和递归思想，跟归并排序差不多，快速排序一般要选择一个基准值(pivot),然后将小于这个基准的放左边，大于这个基准的放右边，基准值放那边无所谓，这样一轮下来，数组分成了2个区域，左边区域比右边区域小，然后对2个区域用递归的方法继续快排。

这里的快速用荷兰国旗问题分成了3个区域，<pivot  | ==pivot | >pivot 然后递归 <pivot 和>pivot的区域 继续分区快排序

关于基准值的选取可以有很多种，可以随机选取，可以最前面的，可以最后面的，这里采用的是最常见(选取最末端元素)

代码

QuickSort ```go func QuickSort(a []int, left int, right int) { if len(a) < 2 || left >= right { return } base := a[right] //基准选取最末端元素 equalArea := PartitionIntSlice(a, left, right, base) QuickSort(a, left, equalArea[0]-1) //递归快排小于区间 QuickSort(a, equalArea[1]+1, right) //递归快排大于区间 } //PartitionIntSlice 给定一个数组，左边界left 右边界right 比较基准base //返回一个2个数值的int数组 该数组第一个值为等于base的开始位置 第二个值为等于base的结束位置 //所以下标小于该数组第一个值的区间都小于base 下标大于数组第二个值的区间都大于base func PartitionIntSlice(a []int, left int, right int, base int) [2]int { l := left - 1 //l为小于区间的结束下标 刚开始指向最小下标左边 r := right + 1 //l为大于区间的开始下标 刚开始指向最大下标右边 cur := left //当前遍历的数设置为整个区间最左边 for cur < r { if a[cur] < base { //如果当前数小于基数 当前数和小于区间的下一个数交换 小于区间扩一个 a[cur], a[l+1] = a[l+1], a[cur] l++ cur++ } else if a[cur] > base { //如果当前数大于基数 则cur下标++ a[cur], a[r-1] = a[r-1], a[cur] r-- } else { //当前数跟基数相等 不变 cur++ } } return [2]int{l + 1, r - 1} } ```

时间复杂度

O(NlogN)

算法稳定性

不稳定

优化

可以选择双轴快排序，也就是选择2个base(不相同,相同的话就又变成了荷兰国旗) 分区为 <minbase | minbase<= && <=maxBase | >maxbase

代码后续补充

网搜图解

计数排序

介绍

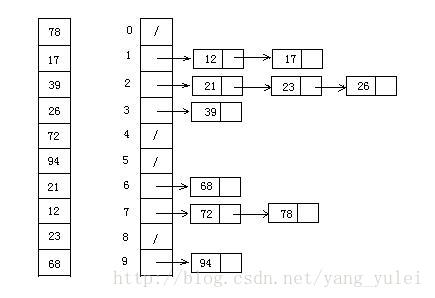
计数排序的应用场景比较清晰，也是桶排序的一种。明确的知道一个数组有N的整数，量比较大，但是数据范围比较小 都是[0,MAX), 然后创建一个计数数组，长度为MAX,计数数组值都初始化为0，然后遍历原数组，将原数组的值和计数数组的下标对应起来，比如原数组某个元素值为1，则计数数组下标为1的元素加1，表示1的元素出现过一次，这个步骤可以叫做入桶。然后顺序遍历计数数组，如果该下标的元素出现过(也就是值>0)，数组元素值为多少，则该下标出桶多少次，依次填回原数组即可。

​

代码

CountingSort ```go func CountSort(a []int, max int) { if len(a) < 2 { return } count := make([]int, max, max) //创建计数的桶 for i := 0; i < len(a); i++ { count[a[i]]++ } indexOfa := 0 for i := 0; i < len(count); i++ { for count[i] > 0 { a[indexOfa] = i indexOfa++ count[i]-- } } } ```

时间复杂度

O(N)

算法稳定性

直接计数排序本身是不稳定的，如果采用累加计数数组，然后倒序遍历原数组结合累加计数数组 则可以实现成稳定的，下面优化版本给出了一个稳定版本

优化

分桶方法可以有很多种，比如0号桶 存放0-9数据  1号桶存放10-19等等都是可以的，每个桶可以再放一个数组 然后对于这个数组进行快排或者插排之类的

如果某个桶数量太大，可以针对这个桶继续分桶等等 这里不再赘述，后续有兴趣再补充。

这里列出一个稳定版本的计数排序

CountSortStable ```go //CountSortStable 桶排序的一种 应用场景 知道一个数组有N个整数 并且范围都是[0 ,MAX) //也就是量大 但是数据范围比较小 稳定版本 采用累加计数数组+倒序遍历原数组 func CountSortStable(a []int, max int) { if len(a) < 2 { return } count := make([]int, max, max) //创建桶 for i := 0; i < len(a); i++ { count[a[i]]++ } //累加计数数组 从下标1开始 其值等于count[i]+count[i-1] for i := 1; i < len(count); i++ { count[i] += count[i-1] //记录原数组元素在原数组出现的最后一个位置 } //然后倒序遍历原数组 这里要用到一个附加数组 help := make([]int, len(a), len(a)) for k := len(a) - 1; k >= 0; k-- { count[a[k]]-- lastIndex := count[a[k]] //这里为了代码好理解 多写一行 help[lastIndex] = a[k] } for i := 0; i < len(help); i++ { a[i] = help[i] } } ```

网搜图解

基数排序

介绍

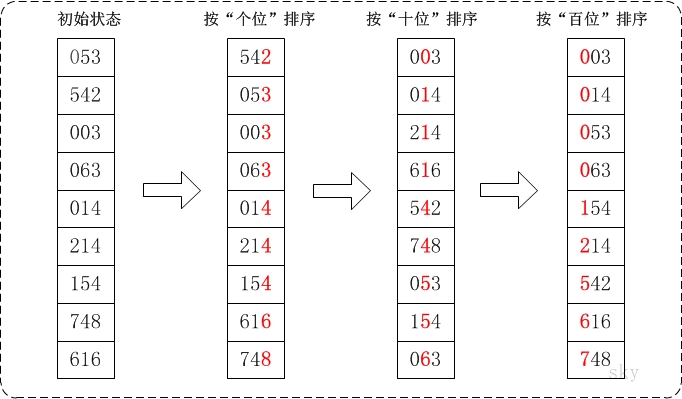
基数排序也是桶排序的一种，主要思想是按照低优先级先排序 然后再按照高优先级再排序，最后完成排序。

比如整数排序，先按照个位排序，再按照十位排序 再按照百位、千位排序，可以参看图解，比较一目了然

代码

RadixSort ```go //GetMax 返回数组中的最大值 func GetMax(a []int) int { max := a[0] for i := 1; i < len(a); i++ { if a[i] > max { max = a[i] } } return max } //radixSort 传入按照什么基数排序 1 个位 10十位 100百位... func radixSort(a []int, radix int) { help := make([]int, len(a), len(a)) //无论是个位、十位、百位... 都只有0-9 10个数字 所以准备10个桶 bucket := make([]int, 10, 10) for i := 0; i < len(a); i++ { radixNum := (a[i] / radix) % 10 //得到某个基数位的数字 比如345 传入radix是1 也就是个位数也就是3 bucket[radixNum]++ } //这个for循环完成 也就完成了个位数桶计数 比如bucket[1]=3 也就是个位数是1的数字有3个 for j := 1; j < len(bucket); j++ { bucket[j] += bucket[j-1] } //这个for循环完成 桶计数含义发生改变 bucket[1]=3表示个位数<=1的数字有3个 //倒序遍历原数组 按照基数位排序后输出到辅助数组 for k := len(a) - 1; k >= 0; k-- { bucket[(a[k]/radix)%10]-- help[bucket[(a[k]/radix)%10]] = a[k] } for i := 0; i < len(a); i++ { a[i] = help[i] } } //RadixSort 基数排序 先按照个位排序 再按照10位排序 再按照百位排序 ... func RadixSort(a []int) { max := GetMax(a) for radix := 1; max/radix > 0; radix *= 10 { radixSort(a, radix) //依次按照个位 十位 百位 ...排序 } } ```

时间复杂度

O(X*2N) 这里的X 主要是指分了多少个基数 比如个位、十位、百位 那X=3 对于每个基数 内部都至少需要2N的时间复杂度

算法稳定性

上面实现的是稳定的 就是采用累加计数 然后倒序遍历数组的方法

优化

待补充

网搜图解

桶排序

介绍

计数排序和基数排序是最常见的2种桶排序思想，不是基于比较的排序思想，桶排序的前提假设大致如下：
  1. 假设原数据是大值均匀分布的 量也比较大
  2. 在原数据上建立1个函数映射关系 将原数据映射到有限个数的桶上
  3. 然后针对每个桶再想办法排序(比如插排、快排等)
  4. 最后按照桶顺序依次输出桶里的元素 就完成了整个排序

代码

这里不写代码了

时间复杂度

去掉常数项就是O(N)

算法稳定性

可以做到稳定

优化

待补充

网搜图解

待补充

排序简单总结

​ 排序稳定性也是特别重要的，因为现实生活中就大量实际应用场景就是要这样，最常用的归并和快排，时间复杂度都是N*logN，归并可以很简单的保持稳定，但快排很难做到稳定，所以工程上经常是基本数据类型的，大容量的排序很可能就是快排了，但如果保存的是自定义类型的数据，大部分是归并排序，而且工程上的排序大都是综合排序，比如<60的规模就直接插入排序了，因为这个时候O($N^2$)的劣势根本体现不出来，常数项操作又非常简单。

​ 工程上往往也不会直接使用递归，因为非常浪费栈空间，很有可能导致栈溢出，还有其它时间浪费问题。

​ 堆排序更重要的是堆这个数据结构，很多地方都会用到堆，比如数组中位数，优先级队列等等。

数组

​ 数组是一种典型的线形数据结构，特点：存放连续的相同数据类型，随机访问速度比较快。随机添加和删除，需要批量移动元素。主流编程语言基本上自身就提供了数组这种数据结构，所以这里不再练习了，数组访问注意边界，动态数组如果是C需要自己实现，C++/go标准库也都提供了动态数组的实现，可以比较方便的访问。

链表

介绍

​ 链表也是一种常用的线形数据结构。特点：空间不是连续的，每个节点除本身数据外，一般都存储至少一个指针数据，指向它的前驱或者后继节点，因为空间不是连续的，所以随机访问效率不高，但是删除，添加效率很高，不需要批量移动元素，这里只简单练习下双向循环链表，单链表更加简单。采用接口的方式实现，练习下go的面向接口编程

代码

DoublyLinkedList_主要接口及结构体定义 接口用结构体指针实现 ```go //LinkNoder 链表接口定义 支持相关操作函数定义 type LinkNoder interface { IsEmpty() bool //返回链表释放为空链表 GetSize() int //返回链表长度 Get(index int) *LinkNode //返回下标对应的元素指针 下标从0开始 GetFirst() *LinkNode //返回第一个元素指针 也就是Head GetLast() *LinkNode //返回最后一个元素指针 也就是Tail //在对应下标位置插入元素 成功返回true 失败返回false InsertByIndex(index int, PayLoad interface{}) bool //默认在最后一个节点后面添加 PushBack(PayLoad interface{}) bool //插入到表头位置 PushFront(PayLoad interface{}) bool //释放包含某个元素 包含(true,下标) 不包含 (false,-1) IsContains(PayLoad interface{}) (bool, int, *LinkNode) //按照下标删除元素 返回元素值 DelByIndex(index int) interface{} DelHead() interface{} //删除头节点 DelTail() interface{} //删除尾节点 //按照元素值删除 成功返回true 失败返回false DelByValue(PayLoad interface{}) bool } //LinkNode 链表节点定义 type LinkNode struct { PayLoad interface{} //节点元素 Prev *LinkNode //前一个节点元素指针 Next *LinkNode //后一个节点元素指针 } //DoublyLinkList 双向循环链表定义 type DoublyLinkList struct { Head *LinkNode //双向循环链表头节点指针(这里指向第一个真正的节点 如果为nil 代表双向循环链表为空) Tail *LinkNode //双向循环链表尾部节点指针 Size int //双向循环链表长度 } ```
DoublyLinkedList详细接口方法实现 ```go //CreateDblist 创建一个空的dblist func CreateDblist() *DoublyLinkList { return &DoublyLinkList{nil, nil, 0} } //DestroyDblist 销毁双向循环链表 func DestroyDblist(dblist *DoublyLinkList) { if dblist.Size == 0 { //如果链表为空直接返回 return } pHead, p := dblist.Head, dblist.Head.Next //pHead指向第一个节点 p指向第一个节点的下一个节点 pHead.Prev, pHead.Next = nil, nil //第一个节点前驱后继都置空 for p != dblist.Head { //遍历将所有节点前驱后继都置空 pNext := p.Next //先记录当前节点的后继 p.Next, p.Prev = nil, nil //当前节点的前驱和后继指针复制为nil 等待gc回收 p = pNext //p指向下一个节点 } } func (dblist *DoublyLinkList) IsEmpty() bool { return dblist.Size == 0 } func (dblist *DoublyLinkList) GetSize() int { return dblist.Size } func (dblist *DoublyLinkList) GetFirst() *LinkNode { return dblist.Head } func (dblist *DoublyLinkList) GetLast() *LinkNode { return dblist.Tail } func (dblist *DoublyLinkList) Get(index int) *LinkNode { if index < 0 || index >= dblist.Size { fmt.Println("index invalid") return nil } p, i := dblist.Head, 0 for ; i < index; i++ { p = p.Next } return p } func (dblist *DoublyLinkList) InsertByIndex(index int, PayLoad interface{}) bool { if index < 0 || index >= dblist.Size { fmt.Println("index invalid") return false } //构造插入元素节点 cur := LinkNode{PayLoad, nil, nil} //当前链表为空 插入第一个元素 if dblist.Size == 0 && index == 0 { dblist.Head = &cur dblist.Tail = &cur cur.Prev = &cur cur.Next = &cur dblist.Size++ return true } if index == 0 { //插入到表头 return dblist.PushFront(PayLoad) } if index == dblist.Size-1 { //插入到表尾 return dblist.PushBack(PayLoad) } //当前链表不为空 先得到index下标元素指针 然后插入 if p := dblist.Get(index); p != nil { cur.Prev, cur.Next = p.Prev, p p.Prev.Next = &cur p.Prev = &cur dblist.Size++ return true } fmt.Println("Get(index) err") return false } func (dblist *DoublyLinkList) PushBack(PayLoad interface{}) bool { //构造插入元素节点 cur := LinkNode{PayLoad, nil, nil} //当前链表为空 插入第一个元素 if dblist.Size == 0 { dblist.Head = &cur dblist.Tail = &cur cur.Prev = &cur cur.Next = &cur dblist.Size++ return true } cur.Prev, cur.Next = dblist.Tail, dblist.Head dblist.Tail.Next = &cur dblist.Head.Prev = &cur dblist.Tail = &cur dblist.Size++ return true } func (dblist *DoublyLinkList) PushFront(PayLoad interface{}) bool { //构造插入元素节点 cur := LinkNode{PayLoad, nil, nil} //当前链表为空 插入第一个元素 if dblist.Size == 0 { dblist.Head = &cur dblist.Tail = &cur cur.Prev = &cur cur.Next = &cur dblist.Size++ fmt.Println("dblist.Size=", dblist.Size) return true } cur.Prev, cur.Next = dblist.Tail, dblist.Head dblist.Head.Prev = &cur dblist.Tail.Next = &cur dblist.Head = &cur dblist.Size++ return true } func (dblist *DoublyLinkList) IsContains(PayLoad interface{}) (bool, int, *LinkNode) { if dblist.Size == 0 { //链表为空 直接返回不存在 return false, -1, nil } for p, i := dblist.Head, 0; i < dblist.Size; p, i = p.Next, i+1 { if p.PayLoad == PayLoad { return true, i, p } } return false, -1, nil } func (dblist *DoublyLinkList) DelHead() interface{} { if dblist.Size == 0 { //链表为空 直接返回不存在 return nil } if dblist.Size == 1 { //如果只有一个元素 删除完链表为空 PayLoad := dblist.Head.PayLoad dblist.Head, dblist.Tail = nil, nil dblist.Size-- return PayLoad } p := dblist.Head p.Next.Prev = dblist.Tail dblist.Tail.Next = p.Next dblist.Head = p.Next p.Prev, p.Next = nil, nil dblist.Size-- return p.PayLoad } func (dblist *DoublyLinkList) DelTail() interface{} { if dblist.Size == 0 { //链表为空 直接返回不存在 return nil } if dblist.Size == 1 { //如果只有一个元素 删除完链表为空 PayLoad := dblist.Tail.PayLoad dblist.Head, dblist.Tail = nil, nil dblist.Size-- return PayLoad } p := dblist.Tail dblist.Head.Prev = dblist.Tail.Prev dblist.Tail.Prev.Next = dblist.Head dblist.Tail = dblist.Tail.Prev p.Prev, p.Next = nil, nil dblist.Size-- return p.PayLoad } func (dblist *DoublyLinkList) DelByIndex(index int) interface{} { if index == 0 { return dblist.DelHead() } if index == (dblist.Size - 1) { return dblist.DelTail() } if p := dblist.Get(index); p != nil { p.Prev.Next = p.Next p.Next.Prev = p.Prev p.Prev, p.Next = nil, nil dblist.Size-- return p.PayLoad } return nil } func (dblist *DoublyLinkList) DelByValue(PayLoad interface{}) bool { _, index, p := dblist.IsContains(PayLoad) if index == 0 { _ = dblist.DelHead() return true } if index == (dblist.Size - 1) { _ = dblist.DelTail() return true } if p != nil { p.Prev.Next = p.Next p.Next.Prev = p.Prev p.Prev, p.Next = nil, nil return true } return false } func (dblist *DoublyLinkList) Print() { fmt.Print("struct DoublyLinkList[") for i, p := 0, dblist.Head; i < dblist.Size; i++ { fmt.Print(p.PayLoad) fmt.Print(",") p = p.Next } fmt.Print("]\n") } ```
## 优化

​ 待补充

​ 按照下标查找元素可以用二分查找

网搜图解

​ 双向循环链表比较简单，很好理解 不再找图了

栈

介绍

​ 栈是一种后进先出的数据结构，可以用很多方式实现，因为我之前的双向循环链表已经实现了，所以直接用其实现了

代码

Stack代码(双向循环链表实现) ```go //HCStack 实现的简易栈 采用双向链表实现 type HCStack struct { Stack *doublylinkedlist.DoublyLinkList } //CreateEmptyStack 创建一个空的栈 func CreateEmptyStack() *HCStack { dblist := doublylinkedlist.CreateDblist() return &HCStack{dblist} } //GetSize 获取栈的真实长度 func (hcstack *HCStack) GetSize() int { return hcstack.Stack.GetSize() } //IsEmpty 返回栈是否为空 func (hcstack *HCStack) IsEmpty() bool { return hcstack.Stack.IsEmpty() } //Push 压栈操作 func (hcstack *HCStack) Push(payLoad interface{}) bool { return hcstack.Stack.PushFront(payLoad) } //Pop 出栈操作 func (hcstack *HCStack) Pop() interface{} { if hcstack.Stack.Size == 0 { fmt.Println("栈为空") return nil } return hcstack.Stack.DelHead() } //Peek 获取栈顶元素 不删除 func (hcstack *HCStack) Peek() interface{} { if hcstack.Stack.Size == 0 { fmt.Println("栈为空") return nil } return hcstack.Stack.GetFirst().PayLoad } //Clear 清空栈 func (hcstack *HCStack) Clear() { doublylinkedlist.DestroyDblist(hcstack.Stack) } ```
# 队列

介绍

​ 队列是一种先进先出的数据结构，可以用很多方式实现，因为我之前的双向循环链表已经实现了，所以直接用其实现了

代码

Queue代码(双向循环链表实现) ```go //HCQueue 实现的简易队列 采用双向链表实现 type HCQueue struct { Queue *doublylinkedlist.DoublyLinkList } //CreateEmptyQueue 创建一个空的栈 func CreateEmptyQueue() *HCQueue { dblist := doublylinkedlist.CreateDblist() return &HCQueue{dblist} } //GetSize 获取队列的真实长度 func (hcqueue *HCQueue) GetSize() int { return hcqueue.Queue.Size } //IsEmpty 返回队列是否为空 func (hcqueue *HCQueue) IsEmpty() bool { return hcqueue.Queue.Size == 0 } //Push 入队列操作 func (hcqueue *HCQueue) Push(payLoad interface{}) bool { return hcqueue.Queue.PushBack(payLoad) } //Pop 出队列操作 func (hcqueue *HCQueue) Pop() interface{} { if hcqueue.Queue.Size == 0 { fmt.Println("Pop 队列为空") return nil } return hcqueue.Queue.DelHead() } //GetHead 获取队头元素 不删除 func (hcqueue *HCQueue) GetHead() interface{} { if hcqueue.Queue.Size == 0 { fmt.Println("GetHead 队列为空") return nil } return hcqueue.Queue.GetFirst().PayLoad } //GetTail 获取队头元素 不删除 func (hcqueue *HCQueue) GetTail() interface{} { if hcqueue.Queue.Size == 0 { fmt.Println("GetTail 队列为空") return nil } return hcqueue.Queue.GetLast().PayLoad } //Clear 清空栈 func (hcqueue *HCQueue) Clear() { doublylinkedlist.DestroyDblist(hcqueue.Queue) } ```
# 二叉树

介绍

​ 二叉树是每个节点最多有2个子树的树结构，有5种基本形态。

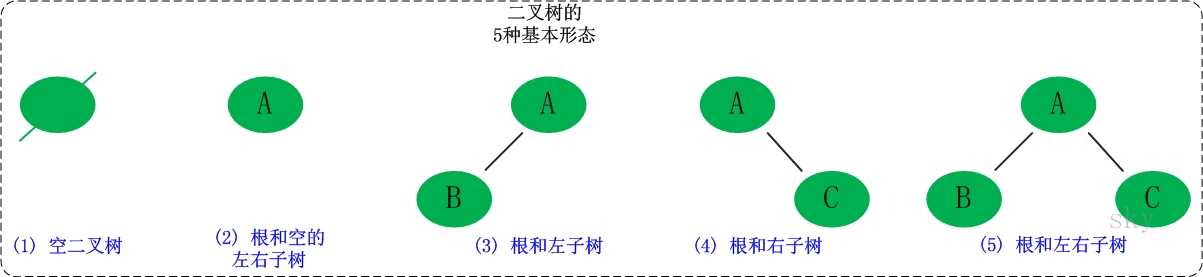
性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。 性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。 性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)

​ 证明：下面用"数学归纳法"进行证明。 (01) 当i=1时，第i层的节点数目为2{i-1}=2{0}=1。因为第1层上只有一个根结点，所以命题成立。 (02) 假设当i>1，第i层的节点数目为2{i-1}。这个是根据(01)推断出来的！ ​ 下面根据这个假设，推断出"第(i+1)层的节点数目为2{i}“即可。 ​ 由于二叉树的每个结点至多有两个孩子，故"第(i+1)层上的结点数目” 最多是 “第i层的结点数目的2倍”。即，第(i+1)层上的结点数目最大值=2×2{i-1}=2{i}。 ​ 故假设成立，原命题得证！

性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)

​ 证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用"性质1"可知，深度为k的二叉树的结点数至多为： 20+21+…+2k-1=2k-1 故原命题得证！

性质3：包含n个结点的二叉树的高度至少为log2 (n+1)

​ 证明：根据"性质2"可知，高度为h的二叉树最多有2{h}–1个结点。反之，对于包含n个节点的二叉树的高度至少为log2(n+1)。

性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1

​ 证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)=“0度结点数(n0)” + “1度结点数(n1)” + “2度结点数(n2)"。由此，得到等式一。 (等式一) n=n0+n1+n2 另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：n1+2n2。此外，只有根不是任何结点的孩子。

​ 故二叉树中的结点总数又可表示为等式二。 (等式二) n=n1+2n2+1 由(等式一)和(等式二)计算得到：n0=n2+1。原命题得证！

满二叉树

​ 高度为h，并且由2{h} –1个结点的二叉树，被称为满二叉树

完全二叉树

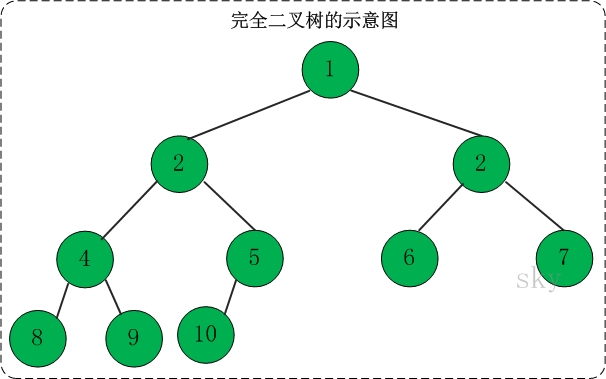
定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。 特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树

二叉查找树

​ 又叫二叉排序树 ,英文一般是binary_search_tree。这里会重点复习下二叉查找树

  • 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 任意节点的左、右子树也分别为二叉查找树。
  • 没有键值相等的节点（no duplicate nodes）

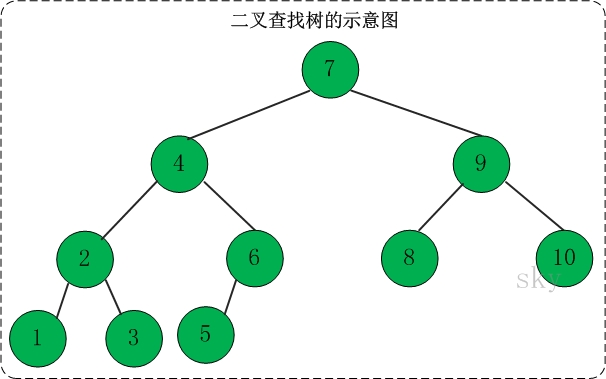
Binary_Search_Tree 二叉查找树

重要概念介绍

  • 一个节点一般有数据域、左孩子指针，右孩子指针，父节点指针

  • 前序遍历

    先遍历根节点 再遍历左子树 再遍历右子树

    如果是递归实现代码如下:

    void preOrder(node* root){
	print(root);
	preOrder(root->left);
	preOrder(root->right);
}

    如果是非递归实现 大值逻辑如下:

    void preOrderNotRecur(node* root){
	stack<node*> myStack;
	myStack.push(root);//将跟压入栈
	while(!myStack.empty()){//栈为空则终止
		node* cur=myStack.pop();
		print(cur);//出栈 并打印
		if( cur->right!=null){
			myStack.push(cur->right);//先压右孩子
		}
		if (cur->left!=null){
			myStack.push(cur->left);//再压左孩子 左孩子先出栈 先打印
		}
	}
}

  • 中序遍历

    先遍历左子树 再遍历根节点 再遍历右子树

    如果是递归实现代码很简单

    void inOrder(node* root){
	inOrder(root->left);
	print(root);
	inOrder(root->right);
}

    如果是非递归实现 大值逻辑如下:

    void inOrderNotRecur(node* root){
	stack<node*> myStack;
	while(root != null){
		myStack.push(root);
		root=root->left;//先将节点自身和节点的所有左孩子全部入栈 最左边的孩子已经入栈 而且是栈顶 
	}
	while(!myStack.empty()){//栈为空则终止
			//弹出以某个节点为根的树的最左边的孩子 该孩子肯定没有左孩子了
			node* cur=myStack.pop();
			print(cur);//出栈 并打印
			if( cur->right!=null){//因为其没有左孩子了 就看看右孩子是否存在
				//如果右孩子不为空 将其右孩子及右孩子的左孩子们全部依次入栈 跟根节点一样的操作
				while(cur != null){
					myStack.push(cur);
					cur=cur->left;//先将节点自身和节点的所有左孩子全部入栈 最左边的孩子已经入栈 而且是栈顶 
					}
			}
	}
}

  • 后序遍历

    先遍历左子树 再遍历右子树 再遍历根节点

    递归实现比较简单

    void postOrder(node* root){
	inOrder(root->left);
	inOrder(root->right);
  print(root);
}

    非递归实现有点麻烦，这里用2个栈实现 ，前序是根左右，如果把前序改为 根右左，该打印的时候全部入到另外一个栈，那么出栈就变为左右根了，也就是实现了后续遍历。

    void postOrderNotRecur(node* root){
	stack<node*> myStack,myStackPrint;
	myStack.push(root);//将根压入栈
	while(!myStack.empty()){//栈为空则终止
		node* cur=myStack.pop();
		myStackPrint.push(cur);//print(cur); 前序对应打印的时候 先压栈到另外一个栈 
		if (cur->left!=null){
			myStack.push(cur->left);//先压左孩子  
		}
    if( cur->right!=null){
			myStack.push(cur->right);//再压右孩子 右孩子先出栈 这里跟前序遍历左右孩子压栈顺序变了下，所以就变为了 根右左
		}
	}
  while( !myStackPrint.empty()){//前面已经按照根右左的顺序入栈 所以出栈就变为了 左右根
    	print(myStackPrint.top());myStackPrint.pop();
  }
}

  • 前驱节点

    小于该节点值中最大的一个节点

  • 后继节点

    大于该节点值中最小的一个节点

  • 插入大概逻辑

      首先要为待插入节点(toIns)找到合适的节点位置，准确来说就是要找到toIns的父节点(parent),然后比较key，判断是左孩子还是右边孩子
  if ( 树为空){直接插入，也就是此节点为根节点 
	}else{ //树不为空
		cur=root //当前节点指向根节点
		while(cur != null){
			parent=cur // toIns的parent也指向当前节点
			if (toIns.key<cur.key){ //小于当前节点的值,当前节点变为其左孩子
				cur=cur.left 
			}
			if (toIns.key>cur.key){ //小于当前节点的值，当前节点变为其右孩子
				cur=cur.right
			}
			if ( key == cur.key ){
				return //不允许插入相同节点
			}
		}
		if toIns.key<parent.key{
			parent->left=toIns
		}else{
			parent->right=toIns
		}
	}

  • 查找前驱节点大概逻辑

     //GetPredecessor 找到当前节点的前驱节点
func (tree *BSTTREE) GetPredecessor(cur *BSTNODE) *BSTNODE {
	var predecessor *BSTNODE = nil
	if cur.Left != nil {
		//如果左子树不为空 则找左子树上面的最大值
		for predecessor = cur.Left; predecessor.Right != nil; predecessor = predecessor.Right {
		}
	} else {
		parent := cur.Parent
		for parent != nil && parent.Right != cur { //如果没有父节点或者如果有父节点并且当前节点是父亲节点的右边孩子 循环终止
			cur, parent = parent, parent.Parent //否则当节节点指向父亲节点 父亲节点指向自己的父亲节点继续判断
		}
		return parent
	}
	return predecessor
}

  • 查找后继节点大值逻辑

    //GetSuccessor 找到当前节点的后继节点
func (tree *BSTTREE) GetSuccessor(cur *BSTNODE) *BSTNODE {
	var successor *BSTNODE = nil
	if cur.Right != nil { //如果右边子树不为空 则找右边子树上面的最小值
		for successor = cur.Right; successor.Left != nil; successor = successor.Left {
		}
	} else {
		parent := cur.Parent
		for parent != nil && parent.Left != cur { //如果没有父节点或者如果有父节点并且当前节点是父亲节点的左孩子 循环终止
			cur, parent = parent, parent.Parent //否则当节节点指向父亲节点 父亲节点指向自己的父亲节点继续判断
		}
		return parent
	}
	return successor
}

  • 删除节点逻辑

    核心逻辑 删除后不能改变二叉树的特点
if (cur为叶子节点){
	 cur.parent.(left|right)=null
	 cur.parent=null
}elseif ( cur有一个孩子)
	//将cur的父亲指向其孩子即可
	cur.parent.(left|right)=cur.(left|right)
	cur.(left|right).parent=cur.parent
	cur.(left|right)=cur.parent=null
}elseif (cur有2个孩子){
	//找到其后继节点 successor
	cur.key=successor.key
	//删除后继节点
	successor.parent.(left|right)=null
	successor.left=successor.right=successor.parent=null
}

代码

BinarySearchTree代码实现 ```go //Less 比较两个元素大小 如果a 0 { myStack.Push(tree.Root) //根节点先压栈 } for myStack.IsEmpty() == false { node := myStack.Pop().(*BSTNODE) //先遍历根节点 if node.Right != nil { myStack.Push(node.Right) //先压右子树 } if node.Left != nil { myStack.Push(node.Left) //再压左子树 } node.Left, node.Right, node.Parent = nil, nil, nil } myStack.Clear() } //CreateBSTree 把接口类型的切片转换为二叉查找树 返回树节点 func CreateBSTree(a []interface{}, less Less) *BSTTREE { tree := &BSTTREE{nil, 0, less} for i := 0; i < len(a); i++ { tree.Insert(a[i]) } return tree } //IsEmpty 判断一个二叉搜索树是否为空 func (tree *BSTTREE) IsEmpty() bool { return tree.Size == 0 } //Insert 插入一个节点 返回是否插入成功 func (tree *BSTTREE) Insert(Key interface{}) bool { toIns := BSTNODE{Key, nil, nil, nil} if tree.Root == nil { //当前树为空 tree.Root = &toIns tree.Size++ return true } //当前树不为空 cur, Parent := tree.Root, tree.Root //Parent指的是待插入节点的父节点 for cur != nil { Parent = cur // toIns的Parent也指向当前节点 if tree.less(toIns.Key, cur.Key) { //小于当前节点的值,当前节点变为其左孩子 cur = cur.Left } else if toIns.Key == cur.Key { return false //不允许插入相同节点 } else { //大于当前节点的值，当前节点变为其右孩子 cur = cur.Right } } tree.Size++ toIns.Parent = Parent if tree.less(toIns.Key, Parent.Key) { Parent.Left = &toIns } else { Parent.Right = &toIns } return true } //SearchKey 查找一个Key是否存在 在则返回其节点地址 不在则返回nil func (tree *BSTTREE) SearchKey(Key interface{}) *BSTNODE { cur := tree.Root for cur != nil && cur.Key != Key { if tree.less(Key, cur.Key) { cur = cur.Left } else { cur = cur.Right } } return cur } //DeleteByKey 删除一个节点 根据传入的节点Key值删除 返回是否删除成功 func (tree *BSTTREE) DeleteByKey(Key interface{}) bool { node := tree.SearchKey(Key) if node != nil { return tree.DeleteByNode(node) } return false //如果node为空 代表Key不在树种 直接返回false } //DeleteByNode 删除一个节点 根据传入的节点地址删除 返回是否删除成功 func (tree *BSTTREE) DeleteByNode(delNode *BSTNODE) bool { if delNode != nil { if delNode.Left == nil { //如果其左子树为空 则用其右孩子替换被删除节点即可 当然如果右孩子是空 也就是纯叶子节点 直接删除即可 fmt.Println("删除节点左子树为空") tree.replaceNode(delNode, delNode.Right) } else if delNode.Right == nil { //如果其右子树为空 则用其左孩子替换被删除节点即可 fmt.Println("删除节点右子树为空") tree.replaceNode(delNode, delNode.Left) } else { fmt.Println("删除节点左右子树都非空") //左右子树都非空 这个时候就找到其后继节点 然后替换 succssor := tree.GetSuccessor(delNode) if succssor.Parent != delNode { //后继节点不是其右孩子(其右孩子还有左子树) fmt.Println("后继节点的父亲节点不是删除节点") //拿后继节点右孩子替换后继节点 也就是后继节点父节点的左孩子 变为后继节点的右孩子 tree.replaceNode(succssor, succssor.Right) succssor.Right = delNode.Right //更新后继节点的右孩子 指向被删除节点的右孩子 delNode.Right.Parent = succssor //同时更新被删除节点右孩子的的Parent属性 } tree.replaceNode(delNode, succssor) //拿后继节点替换被删除节点 succssor.Left = delNode.Left //后继节点的左孩子 指向被删除节点的左孩子 delNode.Left.Parent = succssor //同时更新被删除节点左孩子的Parent属性 } tree.Size-- delNode.Parent, delNode.Left, delNode.Right = nil, nil, nil //等待gc回收 return true } return false } //replaceNode 用newNode替换nodeToRepalce节点 func (tree *BSTTREE) replaceNode(nodeToReplace *BSTNODE, newNode *BSTNODE) *BSTNODE { if nodeToReplace.Parent == nil { //如果被替换的是根节点 则更新根节点指向新的节点 tree.Root = newNode } else if nodeToReplace == nodeToReplace.Parent.Left { //如果被替换节点是其父节点的左孩子 则将其父节点的左孩子指向新的节点 nodeToReplace.Parent.Left = newNode } else { //如果被替换节点是其父节点的右孩子 则将其父节点的右孩子指向新的节点 nodeToReplace.Parent.Right = newNode } if newNode != nil { //如果新的节点非空 则更改其父节点为被替换节点的父节点 newNode.Parent = nodeToReplace.Parent } return newNode } //GetMax 得到树的最大值 func (tree *BSTTREE) GetMax() interface{} { maxNode := tree.Root for ; maxNode.Right != nil; maxNode = maxNode.Right { } if maxNode != nil { return maxNode.Key } return nil } //GetMin 得到树的最小值 func (tree *BSTTREE) GetMin() interface{} { minNode := tree.Root for ; minNode.Left != nil; minNode = minNode.Left { } if minNode != nil { return minNode.Key } return nil } //GetPredecessor 找到当前节点的前驱节点 func (tree *BSTTREE) GetPredecessor(cur *BSTNODE) *BSTNODE { var predecessor *BSTNODE = nil if cur.Left != nil { //如果左子树不为空 则找左子树上面的最大值 for predecessor = cur.Left; predecessor.Right != nil; predecessor = predecessor.Right { } } else { if cur.Parent != nil && cur == cur.Parent.Right { //cur是其父节点的右边孩子 前驱就是其父节点 predecessor = cur.Parent } else if cur.Parent != nil && cur == cur.Parent.Left { // cur是其父节点的左孩子 找到爷爷 并且其父节点是其爷爷的右孩子 if cur.Parent.Parent != nil && cur.Parent.Parent.Right == cur.Parent { predecessor = cur.Parent.Parent } } } return predecessor } //GetSuccessor 找到当前节点的后继节点 func (tree *BSTTREE) GetSuccessor(cur *BSTNODE) *BSTNODE { var successor *BSTNODE = nil if cur.Right != nil { //如果右边子树不为空 则找右边子树上面的最小值 for successor = cur.Right; successor.Left != nil; successor = successor.Left { } } else { if cur.Parent != nil && cur.Parent.Left == cur { // cur是其父节点的左孩子 cur是其父节点的左孩子 successor = cur.Parent } else if cur.Parent != nil && cur.Parent.Right == cur { //cur是其父节点的右孩子 找到爷爷 并且其父节点是其爷爷的左孩子 if cur.Parent.Parent != nil && cur.Parent.Parent.Left == cur.Parent { successor = cur.Parent.Parent } } } return successor } //PreOrder 前序遍历二叉树 打印到屏幕 func (tree *BSTTREE) PreOrder() { a := tree.PreOrderToSlice() fmt.Print("BSTTreePreOrder[") for i := 0; i < len(a); i++ { fmt.Print(a[i].Key) if i == len(a)-1 { fmt.Print("]\n") } else { fmt.Print(",") } } } //InOrder 中序遍历二叉树 打印到屏幕 func (tree *BSTTREE) InOrder() { a := tree.InOrderToSlice() fmt.Print("BSTTreeInOrder[") for i := 0; i < len(a); i++ { fmt.Print(a[i].Key) if i == len(a)-1 { fmt.Print("]\n") } else { fmt.Print(",") } } } //PostOrder 后序遍历二叉树 打印到屏幕 func (tree *BSTTREE) PostOrder() { a := tree.PostOrderToSlice() fmt.Print("BSTTreePostOrder[") for i := 0; i < len(a); i++ { fmt.Print(a[i].Key) if i == len(a)-1 { fmt.Print("]\n") } else { fmt.Print(",") } } } //PreOrderToSlice 前序遍历二叉树 根、左子树、右子树 返回一个slice func (tree *BSTTREE) PreOrderToSlice() []*BSTNODE { if tree.Size == 0 { return nil } a := make([]*BSTNODE, tree.Size) myStack := stack.CreateEmptyStack() myStack.Push(tree.Root) //根节点先压栈 for i := 0; myStack.IsEmpty() == false; { a[i] = myStack.Pop().(*BSTNODE) //先遍历根节点 if a[i].Right != nil { myStack.Push(a[i].Right) //先压右子树 } if a[i].Left != nil { myStack.Push(a[i].Left) //再压左子树 } i++ } myStack.Clear() return a } //InOrderToSlice 中序遍历二叉树 左子树、根、右子树 返回一个slice func (tree *BSTTREE) InOrderToSlice() []*BSTNODE { if tree.Size == 0 { return nil } a := make([]*BSTNODE, tree.Size, tree.Size) myStack := stack.CreateEmptyStack() //先将根节点及其左孩子一条线全部入栈 栈顶最后就是最左的节点 for p := tree.Root; p != nil; p = p.Left { myStack.Push(p) } for i := 0; myStack.IsEmpty() == false; { a[i] = myStack.Pop().(*BSTNODE) //最左边的节点直接出栈 而且其没有左孩子 if i > 0 && tree.less(a[i], a[i-1]) { panic("二叉查找树不正确") } for p := a[i].Right; p != nil; p = p.Left { //将其右孩子及右孩子的左孩子一条线 全部入栈 myStack.Push(p) } i++ } myStack.Clear() return a } //isChildAllVisited 判断当前节点的孩子节点是否都已经访问过了 func isChildAllVisited(p *BSTNODE, visit map[*BSTNODE]int) bool { if p == nil { panic("in isChildAllVisited input *BSTNODE is nil") } childCount := 0 if p.Left != nil { childCount++ } if p.Right != nil { childCount++ } if childCount == 0 { //如果没有孩子 直接返回true return true } if childVisitCount, ok := visit[p]; ok { if childCount == childVisitCount { //所有孩子节点都已经访问过了 delete(visit, p) return true } return false } else { return false //孩子还没有被访问过 } } //PostOrderToSlice 后序遍历二叉树 左子树、右子树、根 返回一个slice func (tree *BSTTREE) PostOrderToSlice() []*BSTNODE { if tree.Size == 0 { return nil } visit := make(map[*BSTNODE]int) //记录某个节点的孩子节点访问次数 a := make([]*BSTNODE, tree.Size) myStack := stack.CreateEmptyStack() myStack.Push(tree.Root) for i := 0; myStack.IsEmpty() == false; { p := myStack.Peek().(*BSTNODE) //当前节点可以理解为根 if isChildAllVisited(p, visit) { //如果当前栈顶节点对应的孩子都已经访问过了 那就出栈 a[i] = myStack.Pop().(*BSTNODE) //fmt.Println("节点:", a[i].Key, " 左右孩子都已经访问过了 已经出栈 当前数组下标为:", i) visit[a[i].Parent]++ i++ continue } if p.Right != nil { //将右孩子压栈 //fmt.Println("当前栈顶是:", p.Key, " 左右孩子尚未访问完成 不出栈，压入右孩子:", p.Right.Key) myStack.Push(p.Right) } if p.Left != nil { //将左孩子压栈 //fmt.Println("当前栈顶是:", p.Key, " 左右孩子尚未访问完成 不出栈，压入左孩子:", p.Left.Key) myStack.Push(p.Left) } } myStack.Clear() return a } ```

​ 其中中序遍历添加了判断是否递增，如果不是递增 则会报错

判断是否是一个BST二叉搜索树 ```go //ISBSTRET 判断是否是BST的返回值 type ISBSTRET struct { isBST bool //是否是BST minValNode *BSTNODE //当前树的最小值节点 maxValNode *BSTNODE //当前树的最大值节点 } //ISBST 判断当前树是否为BST树 外部使用 func ISBST(node *BSTNODE, less Less) bool { ret := isAnBinarySearchTree(node, less) return ret.isBST } //isAnBinarySearchTree 判断当前树是否为BST树 内部使用 func isAnBinarySearchTree(node *BSTNODE, less Less) ISBSTRET { if node == nil { return ISBSTRET{true, nil, nil} } retLeft, retRight := isAnBinarySearchTree(node.Left, less), isAnBinarySearchTree(node.Right, less) if retLeft.isBST && retRight.isBST && (retLeft.maxValNode == nil || less(retLeft.maxValNode.Key, node.Key)) && (retRight.minValNode == nil || less(node.Key, retRight.minValNode.Key)) { ret := ISBSTRET{true, nil, nil} if retLeft.minValNode == nil { ret.minValNode = node } else { ret.minValNode = retLeft.minValNode //当前树的最小值节点赋值为左子树的最小值 } if retRight.maxValNode == nil { ret.maxValNode = node } else { ret.maxValNode = retRight.maxValNode //当前树的最大值节点赋值为右子树的最大值 } return ret } else { fmt.Println("key=", node.Key, " 不是BST") if retLeft.isBST == false { fmt.Println("原因:其左子树不是BST") } if retRight.isBST == false { fmt.Println("原因:其右子树不是BST") } if retLeft.maxValNode != nil && less(retLeft.maxValNode.Key, node.Key) == false { fmt.Println("原因:其左子树存在比其大的节点:", retLeft.maxValNode.Key) } if retRight.minValNode != nil && less(node.Key, retRight.minValNode.Key) == false { fmt.Println("原因:其右子树存在比其小的节点:", retRight.minValNode.Key) } return ISBSTRET{false, nil, nil} } } ```

AVLTree 严格平衡二叉树

介绍

​ AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的。

它是最先发明的自平衡二叉查找树，也被称为高度平衡树。相比于"二叉查找树”，它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。

为什么要有AVL树，因为普通的二叉查找树有可能出现长斜树的情况，最快的情况直接是一棵线形的树，比如依次插入54321，所以这个时候查找的性能大幅下降，不能达到logN,而下降为N，所以才有了AVL，AVL查找的性能达到logN，多付出的代价是插入或者删除的时候要维持平衡，所以需要旋转。

各种旋转示意图

LL旋转实现逻辑

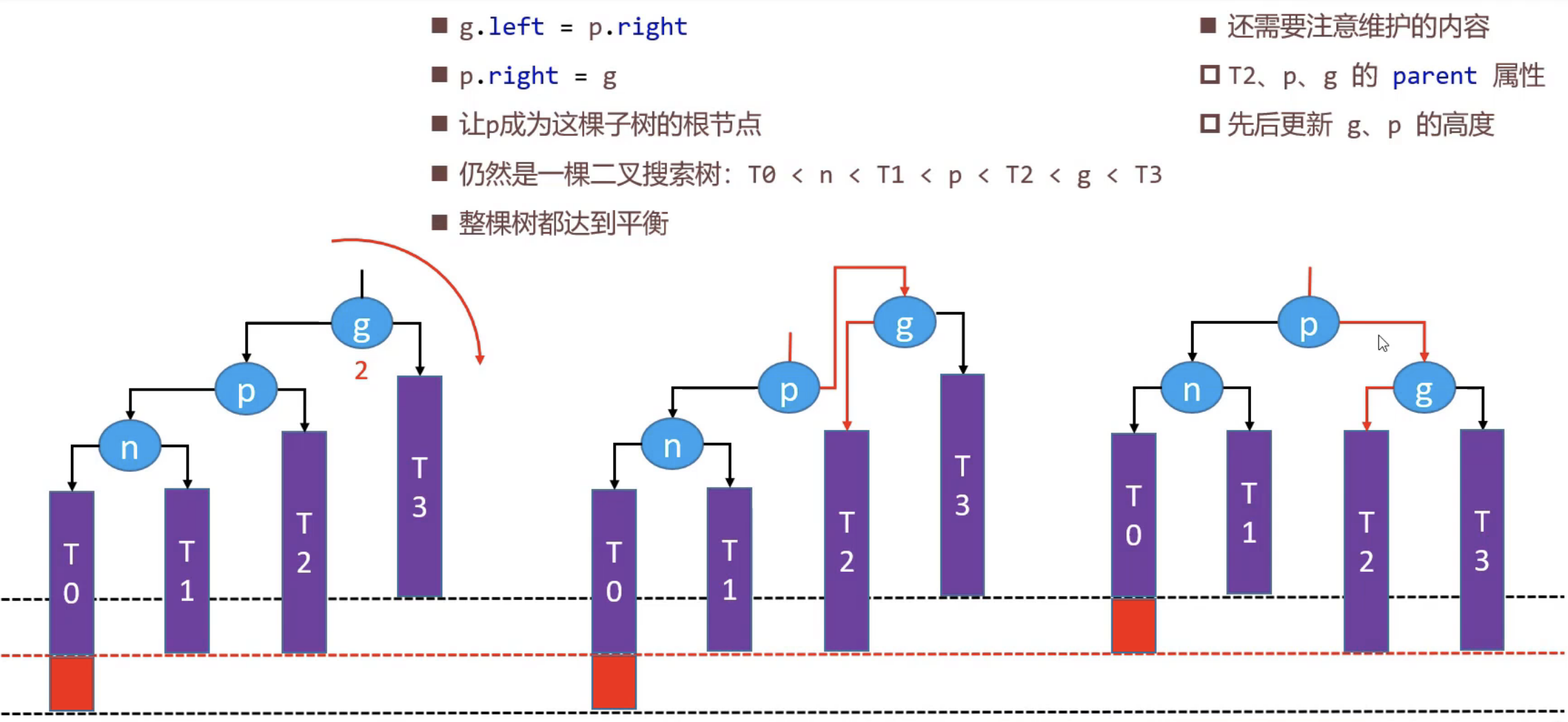
g为待插入节点(红色部分)的爷爷节点 这个节点的平衡性受到破坏 p待插入节点的父节点，同时是爷爷节点的左孩子

//LLRotation LL旋转 旋转一次即可
func (tree *AvlTree) LLRotation(g *AvlTreeNode)
{
  p := g.Left
	gOldParent := g.Parent
	pOldRight := p.Right
	g.Left = pOldRight
	p.Right = g
	//更新相关节点的Parent属性 如果不想要Parent属性 则下面Parent相关代码可以删除
	if pOldRight != nil {
		pOldRight.Parent = g
	}
	if g == tree.Root { //g为根节点
		tree.Root = p
	} else { //g非根节点
		if g == gOldParent.Left {
			gOldParent.Left = p
		} else {
			gOldParent.Right = p
		}
	}
	p.Parent = gOldParent
	g.Parent = p
	//更新g和p的高度
	updateHeight(g)
	updateHeight(p)
	return p
}

RR旋转实现逻辑

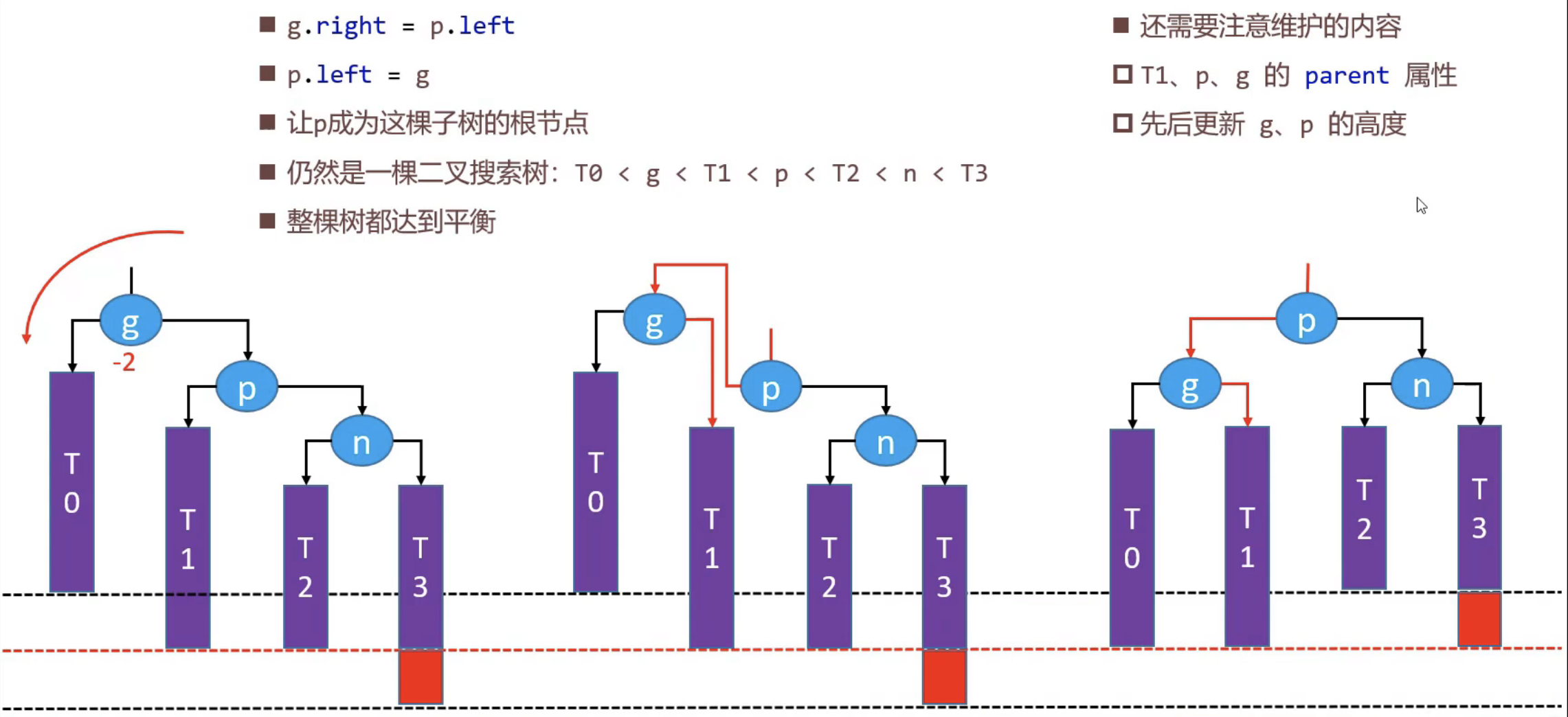
g为待插入节点(红色部分)的爷爷节点 这个节点的平衡性受到破坏 p待插入节点的父节点，同时是爷爷节点的右边

//RRRotation RR旋转 旋转一次即可
func (tree *AvlTree) RRRotation(g *AvlTreeNode)
{
  p := g.Right
	//调整节点左右孩子指向 完成旋转
	gOldParent := g.Parent
	pOldLeft := p.Left
	g.Right = pOldLeft
	p.Left = g
	//更新相关节点的Parent属性 如果不想要Parent属性 则下面Parent相关代码可以删除
	if pOldLeft != nil {
		pOldLeft.Parent = g
	}
	if g == tree.Root { //g为根节点
		tree.Root = p
	} else { //g非根节点
		if g == gOldParent.Left {
			gOldParent.Left = p
		} else {
			gOldParent.Right = p
		}
	}
	p.Parent = gOldParent
	g.Parent = p
	//更新g和p的高度
	updateHeight(g)
	updateHeight(p)
	return p
}

LR旋转实现逻辑

g为待插入节点(红色部分)的爷爷节点 这个节点的平衡性受到破坏 p待插入节点的父节点，同时是爷爷节点的左孩子

这种情况要经过2次旋转 先对p节点RR旋转 再对g节点LL旋转

//LRRotation 2次旋转 先对p节点RR旋转 再对g节点LL旋转
func (tree *AvlTree) LRRotation(g *AvlTreeNode)
{
  g.Left=tree.RRRotation(g.Left)
  return tree.LLRotation(g)
}

RL旋转实现逻辑

g为待插入节点(红色部分)的爷爷节点 这个节点的平衡性受到破坏 p待插入节点的父节点，同时是爷爷节点的右孩子

这种情况要经过2次旋转 先对p节点LL旋转 再对g节点RR旋转

//RLRotation 2次旋转 先对p节点LL旋转 再对g节点RR旋转
func (tree *AvlTree) RLRotation(g *AvlTreeNode)
{
  g.Right=tree.LLRotation(g.Right)
  return tree.RRRotation(g)
}

插入代码

​ 这里先像BST一样先插入，然后针对插入的节点就行平衡性检查和调整 关键就是rebalance函数

AvlTree插入代码 ```go //Insert 插入一个节点 返回插入节点的地址 func (tree *AvlTree) Insert(Key interface{}) *AvlTreeNode { newNode := tree.insertAsBST(Key) //先像BST树一样插入 然后网上逐个判断是否打破平衡因子 做适当调整 if newNode != nil { tree.rebalance(newNode) //调整平衡性 } return newNode } //rebalance 针对一个节点以及所有父辈节点进行平衡性判断与调整 func (tree *AvlTree) rebalance(node *AvlTreeNode) { for node != nil { hLeft, hRight := Height(node.Left), Height(node.Right) if hLeft-hRight == 2 { //左子树比右子树高 可能是LL或者LR if node.Left.Left != nil { // fmt.Println("节点", node.Key, "LL旋转") tree.LLRotation(node) //LL break } else { // fmt.Println("节点", node.Key, "LR旋转") tree.LRRotation(node) //LR break } } else if hLeft-hRight == -2 { if node.Right.Right != nil { // fmt.Println("节点", node.Key, "RR旋转") tree.RRRotation(node) //RR break } else { // fmt.Println("节点", node.Key, "RL旋转") tree.RLRotation(node) //RL break } } else { // fmt.Println(node.Key, "没有打破平衡") updateHeight(node) //没有打破平衡也要更新其高度 } node = node.Parent //逐层往上对每个父辈节点都做判断调整处理 } } func updateHeight(node *AvlTreeNode) { if node == nil { return } hleft, hright := Height(node.Left), Height(node.Right) node.Height = Max(hleft, hright) + 1 } ```

删除代码

这里也是先像BST一样删除，只不过要返回删除后需要重新调整的节点起始位置(其父辈节点 全部高度都要变更，同时做平衡性检查和旋转)

用到的rebalance函数个插入用到的函数一样

AvlTree删除代码 ```go //DeleteByKey 删除一个节点 根据传入的节点值删除 返回是否删除成功 func (tree *AvlTree) DeleteByKey(Key interface{}) bool { var delNode *AvlTreeNode = tree.SearchKey(Key) if delNode != nil { node := tree.deleteByNodeAsBST(delNode) //这里node为需要重新调整高度的起始节点 其父辈都要调整 tree.recomputeHeight(node) tree.rebalance(node) return true } return false } //deleteByNodeAsBST 删除一个节点 根据传入的节点地址删除 返回删除后需要调整高度的第一个节点 其父辈节点都要更新高度 func (tree *AvlTree) deleteByNodeAsBST(delNode *AvlTreeNode) *AvlTreeNode { if delNode != nil { var retNode *AvlTreeNode = nil if delNode.Left == nil { //如果其左子树为空 则用其右孩子替换被删除节点即可 当然如果右孩子是空 也就是纯叶子节点 直接删除即可 // fmt.Println("删除节点左子树为空") tree.replaceNode(delNode, delNode.Right) //这种情况 被删除节点父辈节点都要调整高度 retNode = delNode.Parent } else if delNode.Right == nil { //如果其右子树为空 则用其左孩子替换被删除节点即可 // fmt.Println("删除节点右子树为空") tree.replaceNode(delNode, delNode.Left) //这种情况 被删除节点父辈节点都要调整高度 retNode = delNode.Parent } else { // fmt.Println("删除节点左右子树都非空") //左右子树都非空 这个时候就找到其后继节点 然后替换 succssor := tree.GetSuccessor(delNode) retNode = succssor.Parent //因为后继节点发生变化 if succssor.Parent != delNode { //后继节点不是其右孩子(其右孩子还有左子树) // fmt.Println("后继节点的父亲节点不是删除节点") //拿后继节点右孩子替换后继节点 也就是后继节点父节点的左孩子 变为后继节点的右孩子 tree.replaceNode(succssor, succssor.Right) succssor.Right = delNode.Right //更新后继节点的右孩子 指向被删除节点的右孩子 delNode.Right.Parent = succssor //同时更新被删除节点右孩子的的Parent属性 } tree.replaceNode(delNode, succssor) //拿后继节点替换被删除节点 succssor.Left = delNode.Left //后继节点的左孩子 指向被删除节点的左孩子 delNode.Left.Parent = succssor //同时更新被删除节点左孩子的Parent属性 } tree.Size-- delNode.Parent, delNode.Left, delNode.Right = nil, nil, nil //等待gc回收 return retNode } return nil } //recomputeHeight 节点和其父辈节点全部重新计算高度 func (tree *AvlTree) recomputeHeight(node *AvlTreeNode) { for node != nil { node.Height = Max(Height(node.Left), Height(node.Right)) + 1 node = node.Parent } } ```
判断一个树是否为AVL ```go //ISAVL 判断当前树是否为AVL树 外部使用 func ISAVL(node *AvlTreeNode, less Less) bool { ret := isAnAvlTree(node, less) return ret.isAVL } //isAnAvlTree 判断当前树是否为BST树 内部使用 func isAnAvlTree(node *AvlTreeNode, less Less) ISAVLRET { if node == nil { return ISAVLRET{true, nil, nil, 0} } retLeft, retRight := isAnAvlTree(node.Left, less), isAnAvlTree(node.Right, less) if retLeft.isAVL && retRight.isAVL && (retLeft.maxValNode == nil || less(retLeft.maxValNode.Key, node.Key)) && (retRight.minValNode == nil || less(node.Key, retRight.minValNode.Key)) && ABS(retLeft.height-retRight.height) <= 1 { ret := ISAVLRET{true, nil, nil, Max(retLeft.height, retRight.height) + 1} if retLeft.minValNode == nil { ret.minValNode = node } else { ret.minValNode = retLeft.minValNode //当前树的最小值节点赋值为左子树的最小值 } if retRight.maxValNode == nil { ret.maxValNode = node } else { ret.maxValNode = retRight.maxValNode //当前树的最大值节点赋值为右子树的最大值 } return ret } else { fmt.Println("key=", node.Key, " 不是AVL") if retLeft.isAVL == false { fmt.Println("原因:其左子树不是AVL") } if retRight.isAVL == false { fmt.Println("原因:其右子树不是AVL") } if retLeft.maxValNode != nil && less(retLeft.maxValNode.Key, node.Key) == false { fmt.Println("原因:不是BST 其左子树存在比其大的节点:", retLeft.maxValNode.Key) } if retRight.minValNode != nil && less(node.Key, retRight.minValNode.Key) == false { fmt.Println("原因:不是BST 其右子树存在比其小的节点:", retRight.minValNode.Key) } if ABS(retLeft.height-retRight.height) > 1 { fmt.Println("原因左右子树高度差大于1,左子树高度:", retLeft.height, " 右子树高度:", retRight.height) } return ISAVLRET{false, nil, nil, Max(retLeft.height, retRight.height) + 1} } } ```

RedBalckTree红黑树

介绍

红黑树也是二叉搜索树，也是为了高速查找才发明的，也是为了避免出现二叉搜索树的线形情况，所以想点办法让树尽量平衡，但又不像AVL树那样严格平衡，因为如果要严格平衡，则意味着很有可能随时随地都要调整树，要不断的旋转，这样也会浪费性能，红黑树是一种相对平衡的二叉查找树，有以下特点：

  1. 所有节点都是红色或者黑色
  2. 根节点为黑色
  3. 所有的 NULL 叶子节点都是黑色
  4. 如果该节点是红色的，那么该节点的子节点一定都是黑色
  5. 所有的 NULL 节点到根节点的路径上的黑色节点数量一定是相同的

红黑树保证了最长路径长度不会是最短路径长度的2倍 是一种相对平衡的二叉搜索树

插入

​ 插入相对于删除还是比较简单的 ，还是首先像BST一样插入，然后从插入节点(下面代码记为x)开始做变色和旋转处理，大值的逻辑如下：

1 x.Color=Red //新插入是红色会较大概率不破坏红黑树的特性

2 while( x.Parent.Color==Red){//如果其父亲节点是黑色节点 不会破坏红黑树的性质 之然什么都不用做 直接插入即可
		p,g,u:=x.Parent,x.Parent.Parent,getUncle(x)
	 if getColor(u)==Red{// UncleRed_case
	 		p.Color,u.Color,g.Color=Balck,Black,Red//父节点 叔叔节点变黑色 爷爷节点变红色
	 		x=g//x变为其爷爷节点 继续判断
	 }else{//叔叔节点为空也是黑色
	 		if p==g.Left && x==p.Left{//UncleBlack_LeftLeft_case
	 			p.Color,g.Color=Black,Red
	 			LLRotation(g)
	 		}else if p==g.Left && x==p.Right{//UncleBlack_LeftRight_case
	 			RRRotation(p)//旋转后 x,p亲子关系调换 将p看作新插入节点 x是其父亲 又蜕变成为 Uncle Black LeftLeft case 代码有些许重复但逻辑更清晰
	 			x,p=p,x
	 			p.Color,g.Color=Black,Red
	 			LLRotation(g)
	 		}else if p==g.Right && x=p.Right{ //UncleBlack_RightRight_case
	 			p.Color,g.Color=Black,Red
	 			RRRotation(g)
	 		}else if p==g.Right && x==p.Left{UncleBlack_RightLeft_case
	 				LLRotation(p)//旋转后 x,p亲子关系调换 将p看作新插入节点 x是其父亲 又蜕变成为 Uncle Black RightRight case 代码有些许重复但逻辑更清晰
	 				x,p=p,x
	 				p.Color,g.Color=Black,Red
	 				LLRotation(g)
	 		}
	 }
}
3 Root.Color=Black//将树的根节点染为黑色

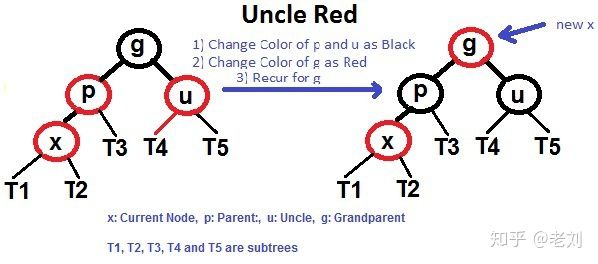
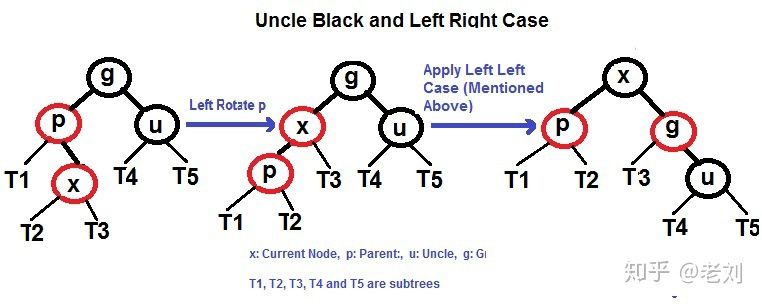
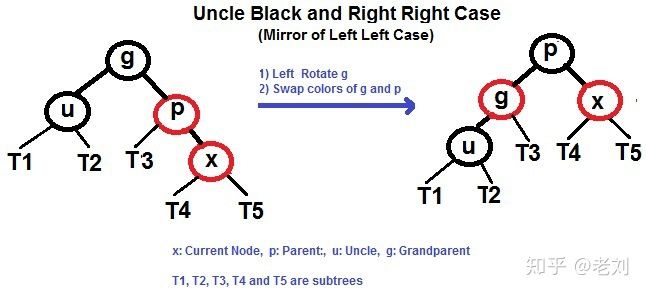
插入代码

红黑树插入代码 ```go //Insert 插入一个节点 返回插入节点的地址 func (tree *RBTree) Insert(Key interface{}) *RBTreeNode { newNode := tree.insertAsBST(Key) //先像BST树一样插入 if newNode != nil { tree.insertFixUp(newNode) //插入节点后调整 } return newNode } //insertFixUp 插入节点后进行颜色调整及旋转相关处理 func (tree *RBTree) insertFixUp(node *RBTreeNode) { // fmt.Println("insertFixUp 当前插入节点为:", node.Key, "Color:", node.Color) for node != tree.Root && node.Parent.Color == Red { //如果其父亲节点是黑色节点 不会破坏红黑树的性质 之然什么都不用做 直接插入即可 p, g, u := node.Parent, node.Parent.Parent, getUncle(node) if getColor(u) == Red { // UncleRed_case p.Color, u.Color, g.Color = Black, Black, Red //父节点 叔叔节点变黑色 爷爷节点变红色 node = g //x变为其爷爷节点 继续判断 } else { //叔叔节点为空也是黑色 if p == g.Left && node == p.Left { //UncleBlack_LeftLeft_case p.Color, g.Color = Black, Red tree.LLRotation(g) } else if p == g.Left && node == p.Right { //UncleBlack_LeftRight_case tree.RRRotation(p) //旋转后 x,p亲子关系调换 将p看作新插入节点 x是其父亲 又蜕变成为 Uncle Black LeftLeft case 代码有些许重复但逻辑更清晰 node, p = p, node p.Color, g.Color = Black, Red tree.LLRotation(g) } else if p == g.Right && node == p.Right { //UncleBlack_RightRight_case p.Color, g.Color = Black, Red tree.RRRotation(g) } else if p == g.Right && node == p.Left { //UncleBlack_RightLeft_case tree.LLRotation(p) //旋转后 x,p亲子关系调换 将p看作新插入节点 x是其父亲 又蜕变成为 Uncle Black RightRight case 代码有些许重复但逻辑更清晰 node, p = p, node p.Color, g.Color = Black, Red tree.RRRotation(g) } } } if tree.Root == node { //如果插入或者调整后当前节点是根节点 则将其置为黑色 node.Color = Black } } ```

删除

​ 删除根插入比较相对复杂，但无非也是穷举的过程

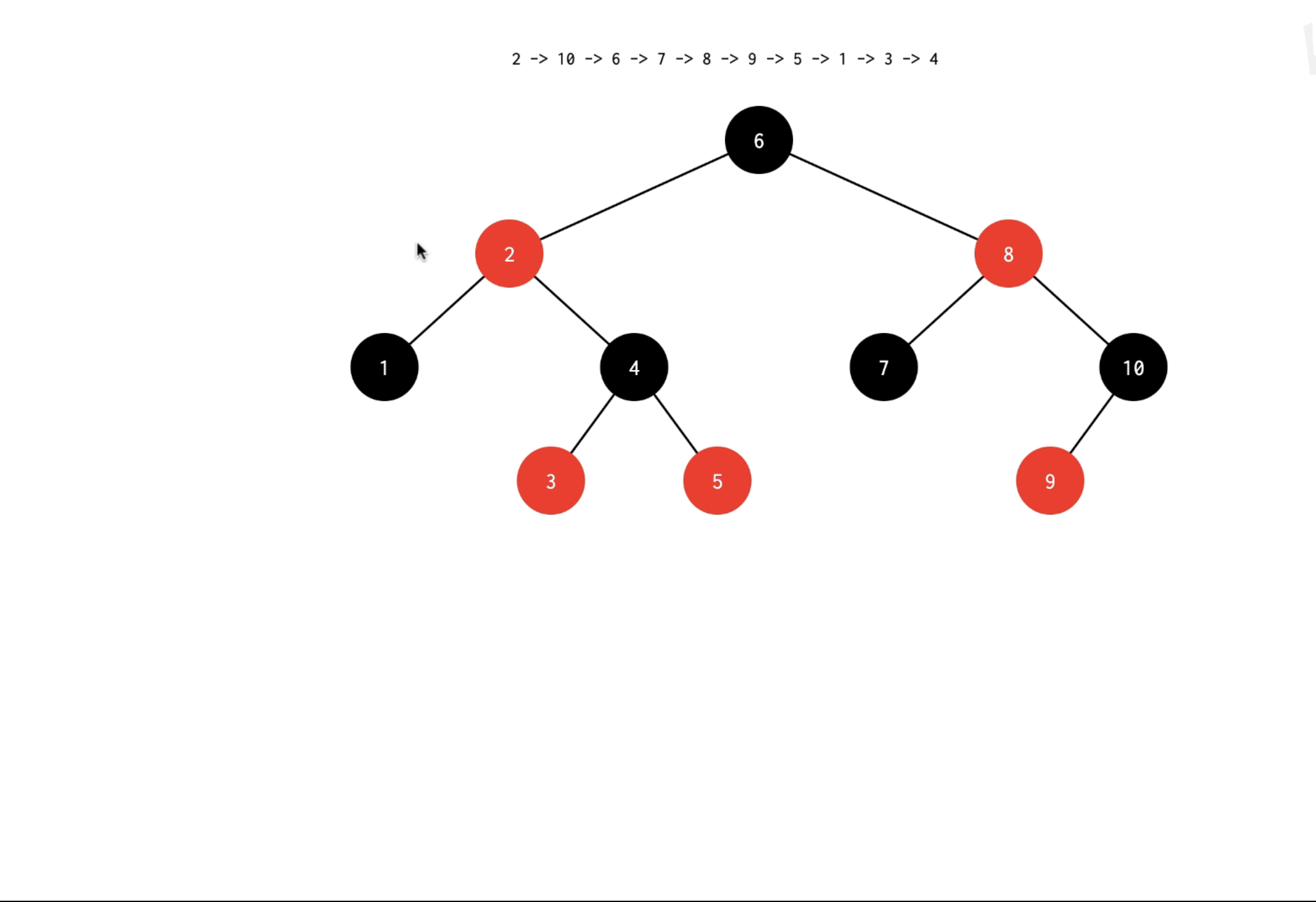
删除的节点只能存在三种情况：
caseA:被删除节点是叶子节点(如图中的1,3,5,7,9){
	A1:如果叶子节点是红色的，直接删除即可，无需修复 不会破坏红黑树特性
	A2:如果叶子节点是黑色，删除后会破坏特性5 需要修复
}
caseB:被删除节点只有一个孩子(如图中的10){
	 p为被删除节点 parent,c为其孩子节点 child
	 B1:p为黑色,c为红色 {//如图中的10和9 删除10节点
	 		交换p和c的值，然后将删除节点改为c,因为是红色，变成了A1，直接删除即可，不论孩子是左孩子还是右孩子都是一样的
	 }
	 B2:p为黑色,c为黑色{
	 		交换p和c的值，然后将删除节点改为c,也就变成了A2的情况
	 }
}
caseC:被删除节点有2个孩子{//如图中的2,4,6,8
		找到被删除节点的后继节点，然后交换被删除节点和其后继节点的值
		然后将删除节点改为其后继节点(要么是叶子节点 对应caseA,要么是只有右孩子 对应caseB)
}
综合上面的情况 caseC可以转化为caseB,caseB又可以转为为caseA A1情况可以直接删除，所以只有A2需要重点关注，当然也是最复杂的。很多穷举情况，上网找了一张图应该是比较全面的，也比较好理解，多看几遍就记住了。

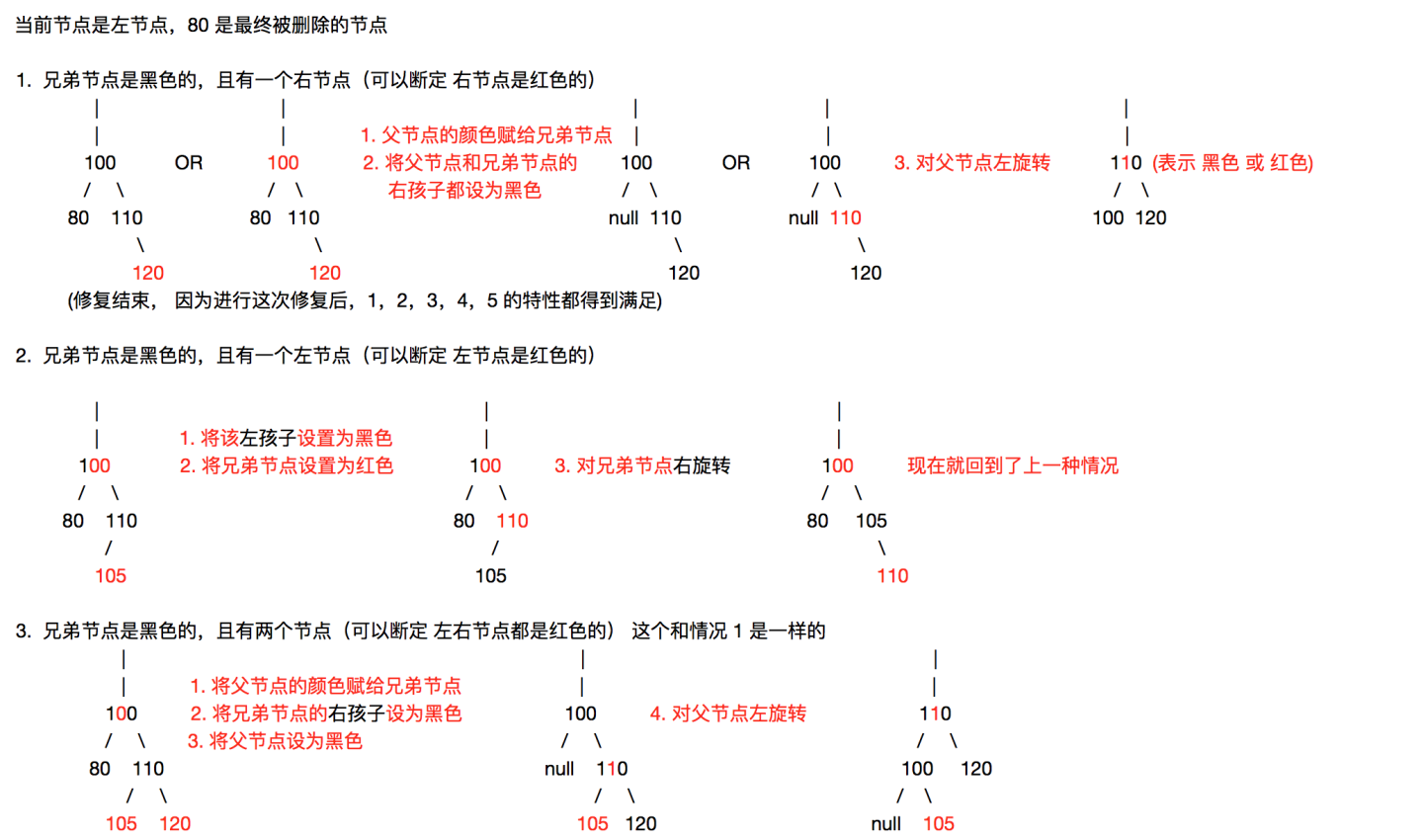
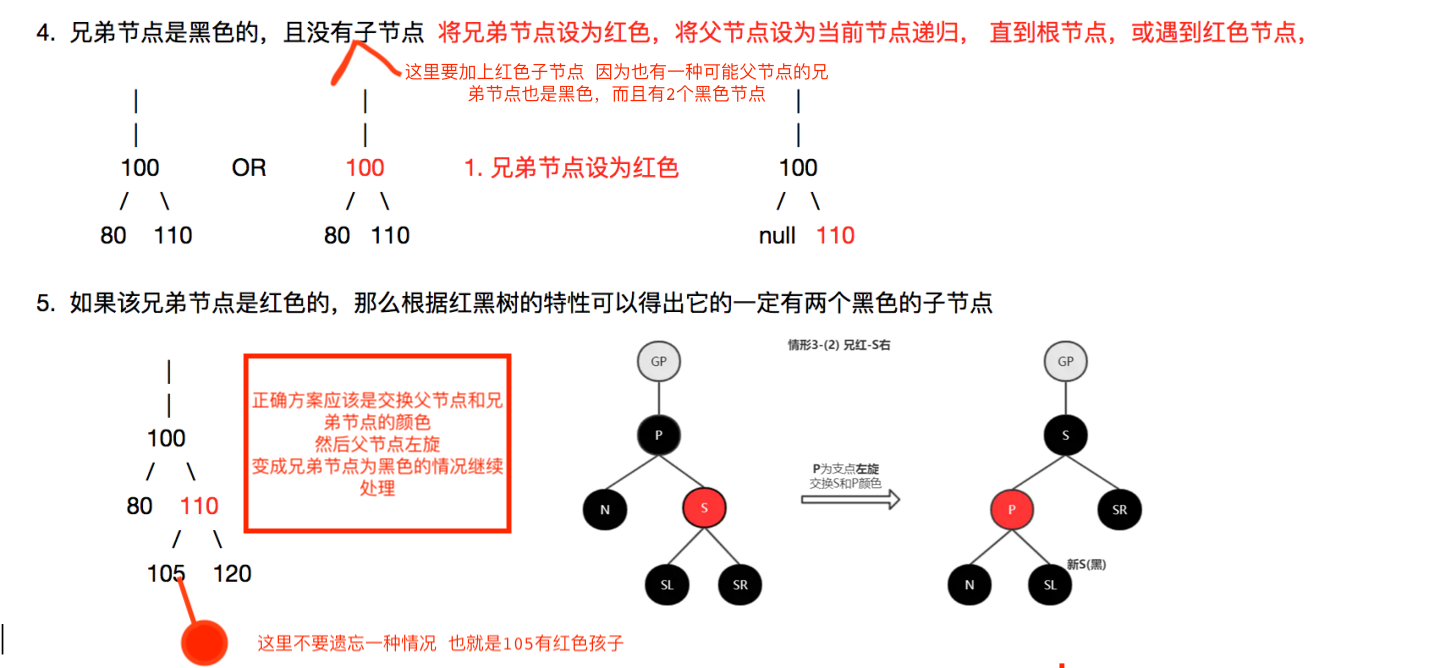
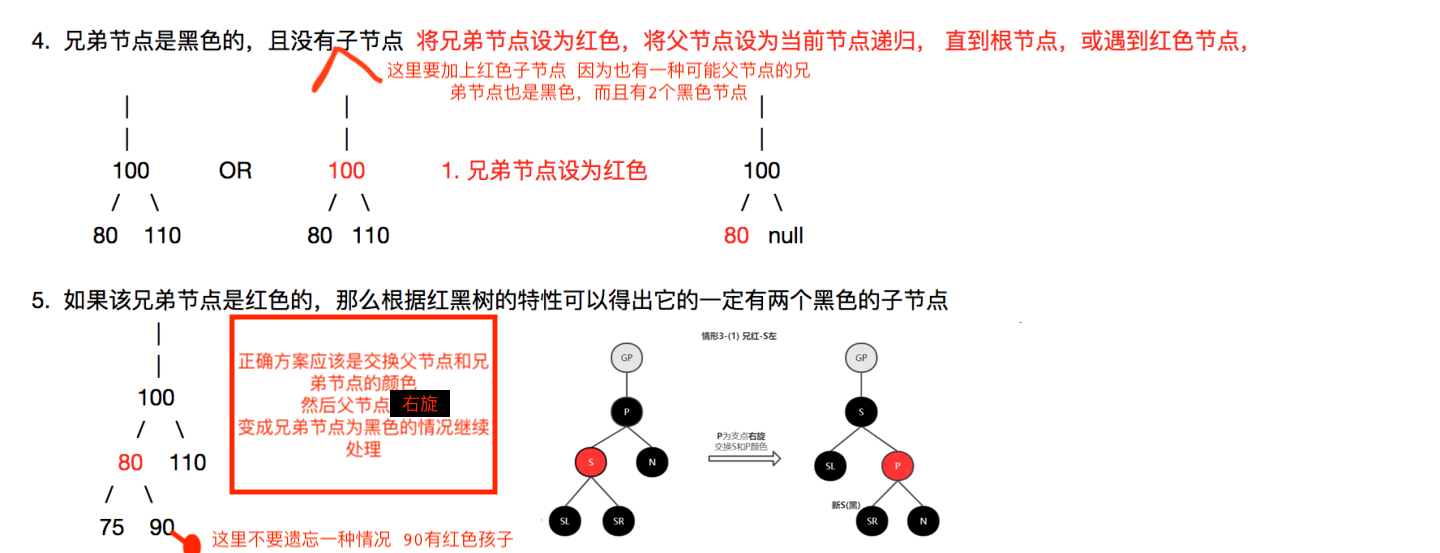
删除代码

红黑树删除核心代码 ```go //DeleteByKey 删除一个节点 根据传入的节点值删除 返回是否删除成功 func (tree *RBTree) DeleteByKey(Key interface{}) bool { var delNode *RBTreeNode = tree.SearchKey(Key) //先找到被删除的节点 if delNode != nil { if delNode.Left == nil && delNode.Right == nil { //caseA:被删除节点是叶子节点 return tree.delLeafNode(delNode) } else if delNode.Right == nil || delNode.Left == nil { //caseB:被删除节点只有一个孩子 return tree.delNodeHasOneChild(delNode) } else { //caseC:被删除节点有2个孩子 return tree.delNodeTwoOneChild(delNode) } } return false } //delLeafNode 删除叶子节点 对应删除的caseA:被删除节点是叶子节点 func (tree *RBTree) delLeafNode(delNode *RBTreeNode) bool { if delNode.Color == Red { //A1:如果叶子节点是红色的，直接删除即可，无需修复 不会破坏红黑树特性 p := delNode.Parent //肯定有父节点 因为只有根节点没有父节点 但根节点是黑色 if delNode == p.Left { p.Left = nil } else { p.Right = nil } tree.Size-- } else { //A2:如果叶子节点是黑色，删除后会破坏特性5 需要修复 tree.delBlackLeafFixUp(delNode) } return true } //delNodeHasOneChild 删除只有一个孩子节点的情况 对应caseB:被删除节点只有一个孩子 func (tree *RBTree) delNodeHasOneChild(delNode *RBTreeNode) bool { c := delNode.Left //c指向其孩子节点 if c == nil { c = delNode.Right } if delNode.Color == Black && c.Color == Red { //B1:p为黑色,c为红色 交换p和c的值，然后将删除节点改为c,因为是红色，变成了A1，直接删除即可 delNode.Key, c.Key = c.Key, delNode.Key delNode.Left, delNode.Right = nil, nil //删除其孩子节点 c.Left, c.Right, c.Parent = nil, nil, nil } else if c.Color == Black { //B2:p为黑色或者红色,c为黑色 交换p和c的值，然后将删除节点改为c,也就变成了A2的情况 delNode.Key, c.Key = c.Key, delNode.Key tree.delBlackLeafFixUp(c) } tree.Size-- return true } //delNodeTwoOneChild 删除节点有2个孩子的情况 对应caseC:被删除节点有2个孩子 func (tree *RBTree) delNodeTwoOneChild(delNode *RBTreeNode) bool { //找到被删除节点的后继节点，然后交换被删除节点和其后继节点的值 然后将删除节点改为其后继节点(要么是叶子节点 对应caseA,要么是只有右孩子 对应caseB) successor := tree.GetSuccessor(delNode) delNode.Key, successor.Key = successor.Key, delNode.Key if successor.Right != nil { //后继节点右孩子不为空 左孩子肯定为空 蜕变为caseB return tree.delNodeHasOneChild(successor) } //后继节点为叶子节点 蜕变为caseA return tree.delLeafNode(successor) } //删除黑色叶子节点并调整 返回删除节点的位置 func (tree *RBTree) delBlackLeafFixUp(delNode *RBTreeNode) { oldDeleteNode := delNode //记录传入的节点 因为case4会改变其值 等调整完毕 再将其父节点指向它的指针改为nil 交给gc回收 tree.Size-- if delNode == tree.Root { //如果被删除节点是root节点 而且是叶子节点 说明整个树只剩下1个root节点了 直接删除即可 tree.Root = nil } else { for delNode != tree.Root && delNode.Color == Black { p, b := delNode.Parent, getBrother(delNode) if delNode == p.Left { //当前节点是左节点 if b.Color == Red { //case5 : 如果该兄弟节点是红色的，那么根据红黑树的特性可以得出它的一定有两个黑色的子节点 b.Color, p.Color = Black, Red tree.RRRotation(p) } else { if b.Right != nil && b.Right.Color == Red { //case1和case3 //对应case1 : 兄弟节点是黑色的，且有一个右节点（可以断定 右节点是红色的 //也对应case3 : 兄弟节点是黑色的，且有两个节点（可以断定 左右节点都是红色的）这两种情况一样 b.Color, p.Color = p.Color, b.Color //交换兄弟节点和父节点的颜色 b.Right.Color = Black tree.RRRotation(p) break } else if b.Left != nil && b.Left.Color == Red { //case2 //对应case2: 兄弟节点是黑色的，且有一个左节点（可以断定 左节点是红色的） b.Left.Color, b.Color = Black, Red tree.LLRotation(b) //经过LL旋转也就是右旋 就蜕变为了case1 } else { //case4:兄弟节点是黑色的，且没有红色子节点 b.Color = Red if p.Color == Red { //将父节点直接染黑就结束了 也就是相当于父子颜色交换 黑色节点个数不变 p.Color = Black break } else { delNode = p //将删除节点改为其父亲节点 递归,直到遇到根节点 或者其父亲节点是红色的 } } } } else { //当前节点是右孩子 if b.Color == Red { //case5: 如果该兄弟节点是红色的，那么根据红黑树的特性可以得出它的一定有两个黑色的子节点 b.Color, p.Color = Black, Red tree.LLRotation(p) } else { if b.Left != nil && b.Left.Color == Red { //case1和case3 //对应case1 : 兄弟节点是黑色的，且有一个右节点（可以断定 右节点是红色的 //也对应case3 : 兄弟节点是黑色的，且有两个节点（可以断定 左右节点都是红色的）这两种情况一样 b.Color = p.Color p.Color, b.Left.Color = Black, Black tree.LLRotation(p) break } else if b.Right != nil && b.Right.Color == Red { //case2 //对应case2: 兄弟节点是黑色的，且有一个左节点（可以断定 左节点是红色的） b.Right.Color, b.Color = Black, Red tree.RRRotation(b) //经过RR旋转也就是右旋 就蜕变为了case1 } else { //case4:兄弟节点是黑色的，且没有红色子节点 b.Color = Red if p.Color == Red { //将父节点直接染黑就结束了 也就是相当于父子颜色交换 黑色节点个数不变 p.Color = Black break } else { delNode = p //将删除节点改为其父亲节点 递归,直到遇到根节点 或者其父亲节点是红色的 } } } } } } //颜色调整和旋转完毕 将oldDeleteNode对应父节点指向它的指针改为nil 等待gc回收 if oldDeleteNode == oldDeleteNode.Parent.Left { oldDeleteNode.Parent.Left = nil } else { oldDeleteNode.Parent.Right = nil } } ```

判断是否是红黑树

检查一个树是否是红黑树 ```go //ISRBTRET 判断是否是RBT的返回值 type ISRBTRET struct { ISRBT bool //是否是RBT minValNode *RBTreeNode //当前树的最小值节点 maxValNode *RBTreeNode //当前树的最大值节点 BlackCount int //左右子树路径的黑色节点个数这里应该相同 否则就不是红黑树 } //ISRBT 判断当前树是否为AVL树 外部使用 func ISRBT(node *RBTreeNode, less Less) bool { if node == nil { return true } if node.Color == Red { return false } ret := isAnRBTree(node, less) return ret.ISRBT } //isAnRBTree 判断当前树是否为BST树 内部使用 func isAnRBTree(node *RBTreeNode, less Less) ISRBTRET { if node == nil { return ISRBTRET{true, nil, nil, 0} } if node.Color == Red && (getColor(node.Left) == Red || getColor(node.Right) == Red) { fmt.Println("不是RBT 原因是节点:", node.Key, " 颜色为红,其子节点还有红色") if getColor(node.Left) == Red { fmt.Println("左孩子为红色:", node.Left.Key) } if getColor(node.Right) == Red { fmt.Println("右孩子为红色:", node.Right.Key) } return ISRBTRET{false, nil, nil, 0} } retLeft, retRight := isAnRBTree(node.Left, less), isAnRBTree(node.Right, less) if retLeft.ISRBT && retRight.ISRBT && (retLeft.maxValNode == nil || less(retLeft.maxValNode.Key, node.Key)) && (retRight.minValNode == nil || less(node.Key, retRight.minValNode.Key)) && retLeft.BlackCount == retRight.BlackCount { blackCount := retLeft.BlackCount if node.Color == Black { //如果当前节点是黑色 黑色节点数量加一 blackCount++ } ret := ISRBTRET{true, nil, nil, blackCount} if retLeft.minValNode == nil { ret.minValNode = node } else { ret.minValNode = retLeft.minValNode //当前树的最小值节点赋值为左子树的最小值 } if retRight.maxValNode == nil { ret.maxValNode = node } else { ret.maxValNode = retRight.maxValNode //当前树的最大值节点赋值为右子树的最大值 } return ret } else { fmt.Println("key=", node.Key, " 不是RBT") if retLeft.ISRBT == false { fmt.Println("原因:其左子树不是RBT") } if retRight.ISRBT == false { fmt.Println("原因:其右子树不是RBT") } if retLeft.maxValNode != nil && less(retLeft.maxValNode.Key, node.Key) == false { fmt.Println("原因:不是BST 其左子树存在比其大的节点:", retLeft.maxValNode.Key) } if retRight.minValNode != nil && less(node.Key, retRight.minValNode.Key) == false { fmt.Println("原因:不是BST 其右子树存在比其小的节点:", retRight.minValNode.Key) } if retLeft.BlackCount != retRight.BlackCount { fmt.Println("原因左右子树黑色节点个数不相等,左子树黑节点个数:", retLeft.BlackCount, " 右子树黑节点个数:", retRight.BlackCount) } return ISRBTRET{false, nil, nil, -1} } } ```

从上到下按照层次 从左到右按照顺序打印红黑树 红色节点打印红色

逐层，每层从左到右形象化打印红黑树 ```go //PrintVisually 逐层打印 方向 从左往右形象化更直观的打印二叉树 func (tree *RBTree) PrintVisually() { if tree.Size == 0 { return } nilNode := &RBTreeNode{nil, nil, nil, nil, false} //定义一个空节点 depth := getMaxDepth(tree.Root) //最深层次 // fmt.Println("depth=", depth) //申请2个队列 从1个队列出队 同时将其左右子树依次入队到另外一个队列 myQueue1, myQueue2 := queue.CreateEmptyQueue(), queue.CreateEmptyQueue() myQueue1.Push(tree.Root) //根节点先入队列1 //终止条件 最大层次打印完毕 for i, cur, next := 1, myQueue1, myQueue2; i <= depth; i, cur, next = i+1, next, cur { count := 1 //标记打印当前层次的第几个元素 tabCount := (1<<(depth+1-i) - 1) / 2 //打印元素 计算打印前面\t个数 for cur.IsEmpty() == false { //队列1不为空 if count > 1 { tabCount = (1<<(depth+1-i) - 1) } node := cur.Pop().(*RBTreeNode) if node != nilNode { //不是空节点 //将其左右孩子入到下一层队列 for j := 0; j < tabCount; j++ { fmt.Print(" ") } if node.Color == Red { fmt.Print(redBg, node.Key, reset) } else { fmt.Print(node.Key) } count++ if node.Left != nil { next.Push(node.Left) } else { next.Push(nilNode) //加入一个空节点 为了打印好看 } if node.Right != nil { next.Push(node.Right) } else { next.Push(nilNode) //加入一个空节点 为了打印好看 } } else { //空节点 for j := 0; j < tabCount; j++ { fmt.Print(" ") } fmt.Print("*") count++ next.Push(nilNode) //加入一个空节点 为了打印好看 next.Push(nilNode) //加入一个空节点 为了打印好看 } } fmt.Print("\n") } myQueue1.Clear() myQueue2.Clear() } ```

B树

定义及特点

​ B树也叫B-树 这里的-是连接符，不是减号，是一个多路平衡查找树，描述一个B树必须要说明是几阶的，也就是树中一个节点最多能有多少个孩子，一般用m来表示，如果m=2，那就是AVL树（当然也是BST树）

一颗m阶的B树定义及特点如下：

  1. 每个结点最多有m-1个关键字。

  2. 根结点至少要有1个关键字(也就是2个孩子)。

  3. 非根结点至少有 取上限(m/2)-1个关键字。如果是4阶，则至少有1个关键字，如果是5阶，则至少有2个关键字

  4. 每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。

  5. 所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。

下面有个5阶B树示意图

B树主要是为了解决磁盘存储高效查找的，如果是AVL树，对于在内存或者少量在磁盘存放还是可以接受的，但是如果大量文件存放在磁盘上面，因为是2路的，所以势必avl的高度值就很大，这个高度简单来说就是代表磁盘查找的次数，磁盘的速度远远低于内存速度，所以如果是大量数据存放在磁盘，AVL的效率就肯定是不行的了。所以实际应用中B树阶树一般都比较大，通常都是100往上，因为这样可以降低树的高度，当然也就减少了磁盘搜索次数，提高查找性能。

MangoDb是B树索引，Mysql是B+树索引。上图中的data实际中往往是磁盘的地址，这里为了简单期间，数据也全部放到内存。后续有时间实现个B+树存放在磁盘的key-value简易数据库

本章节大部分图片来自：https://www.cnblogs.com/nullzx/p/8729425.html

插入操作简易介绍

​ 这里的插入指的是插入一对key-value,如果key已经存在，那就更新value。B树的插入有一个特点就是首先肯定是在叶子节点完成插入操作的(最底层的节点)

  1. 先根据key找到对应的要插入的叶子节点并按照大小顺序插入(小值在前面)

  2. 判断插入后的叶子节点key值个数是否<=m-1,如果是 则直接结束插入操作，否则继续下一步分裂调整

  3. 如果插入后叶子节点key值个数>m-1 则不符合特点1,需要调整 3.1. 找到该节点中间的key记为midKey，可以用二分的mid方法，begin+(end-begin)/2 3.2. 以midkey为中心，其左其右各分裂一个节点出来 记为midLeft,midRight

    3.3. 将midKey插入到该叶子节点的父节点中(小值在前面) 同时其左分支指向midLeft 右分支指向midRight

    3.4. 将指针指向其父节点(调整后midKey在的节点) 继续循环第2、3步判断—因为父节点新插入一个midKey后也可能破坏特点1

网搜简易插入图解m=5

  1. 空树插入39

    网上的图是先直接申请好节点空间，也就是5阶最多4个key，当然也可以用链表存放，用的时候再生成。 这个时候只有一个节点也是根节点

  2. 继续插入22、97、41

    因为key个数没有超过m-1，所以直接按序插入即可。无序分裂调整

  3. 继续插入53

    这时候key个数超过m-1，就需要找到中间key,然后分裂调整，midKey为41，

    分裂为midLeft(22,39),midRight(53,97),将midKey 41,插入到其父节点，这里因为父节点为空，所以41成为新的根节点 左边指向midLeft,右边指向midRight。

    将指针指向父节点，也就是41在的新的root节点，继续判断，发现key值数量<=m-1 循环中断，插入分裂调整结束，调整后图如下:

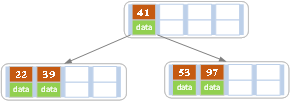
  4. 更多例子 请直接看https://www.cnblogs.com/nullzx/p/8729425.html

插入代码

BTree插入代码go版本 ```go //Less 比较两个元素大小 如果a index; i-- { //从index位置开始的所有元素指针后移一位 btNode.Nodes[i] = btNode.Nodes[i-1] } btNode.Nodes[index] = node //插入节点 btNode.KeyNum++ if btNode.KeyNum < tree.M { //如果插入元素后关键词数量没有超过最大值 直接返回 fmt.Println("key:", node.Key, "插入后当前节点关键词数量为", btNode.KeyNum, "没有超过最大关键词数量:", tree.M-1) return true } //如果插入元素后关键词数量刚好超过最大值 则对本节点做分裂操作 for btNode.KeyNum >= tree.M { fmt.Println("key:", node.Key, "插入后当前节点关键词数量为", btNode.KeyNum, "超过最大关键词数量:", tree.M-1) fmt.Println("开始分裂调整") btNode = tree.split(btNode) } return true } //split 对btNode做分裂调整 返回调整后的父节点 func (tree *BTree) split(btNode *BTNode) *BTNode { midIndex := 0 + (btNode.KeyNum-1)/2 midNode := btNode.Nodes[midIndex] //0--minIndex-1 是分裂后的左节点(还在原来的节点中) midIndex+1到btNode.KeyNum-1是分裂后的右节点(生成一个新的节点) //先生成右节点 rightBtNode := tree.CreateNewBTNode(nil, btNode.Nodes[midIndex+1:], btNode.Childs[midIndex+1:]) //如果新生成的右节点本身有孩子节点 则将其孩子节点的父亲节点改为新生成的节点 if rightBtNode.Childs[0] != nil { for i := 0; i <= rightBtNode.KeyNum; i++ { rightBtNode.Childs[i].Parent = rightBtNode } } //再将原节点中所有右节点的数据清除 for i := midIndex; i < len(btNode.Nodes); i++ { btNode.Nodes[i] = nil btNode.KeyNum-- } for i := midIndex + 1; i < len(btNode.Childs); i++ { btNode.Childs[i] = nil } //将midIndex插入到父节点 parentBtNode := tree.insertIntoParent(btNode.Parent, midNode, btNode, rightBtNode) return parentBtNode } //insertIntoParent 将node插入到父亲节点 func (tree *BTree) insertIntoParent(parentBtNode *BTNode, node *Node, leftBtNode *BTNode, rightBtNode *BTNode) *BTNode { if parentBtNode == nil { //是根节点分裂的 因为其父节点为nil 生成一个新的节点 将node插入 并指向传入的左右子树 并将根节点指向新生成的节点 fmt.Println("根节点分裂") btNode := tree.CreateNewBTNode(nil, nil, nil) btNode.Nodes[0] = node btNode.Childs[0], btNode.Childs[1] = leftBtNode, rightBtNode btNode.KeyNum++ leftBtNode.Parent, rightBtNode.Parent = btNode, btNode tree.Root = btNode return btNode } //如果传入父亲节点不为空 则先找到应该插入的位置 index := -1 for i := 0; i < parentBtNode.KeyNum; i++ { fmt.Println(node.Key, "父节点 ", i, "位置", parentBtNode.Nodes[i].Key) if tree.less(node.Key, parentBtNode.Nodes[i].Key) { index = i break } if i == parentBtNode.KeyNum-1 { index = i + 1 //如果已经是最后一个节点 则插入到最后的位置 break } } fmt.Println(node.Key, "将插入到父节点的", index, "位置") for i := len(parentBtNode.Nodes) - 1; i > index; i-- { parentBtNode.Nodes[i] = parentBtNode.Nodes[i-1] //index后面元素后移一位 } parentBtNode.Nodes[index] = node //完成节点插入 for i := len(parentBtNode.Childs) - 1; i > (index + 1); i-- { parentBtNode.Childs[i] = parentBtNode.Childs[i-1] } parentBtNode.Childs[index] = leftBtNode parentBtNode.Childs[index+1] = rightBtNode rightBtNode.Parent = parentBtNode parentBtNode.KeyNum++ return parentBtNode } //CreateNewBTNode 初始化一个BTNode func (tree *BTree) CreateNewBTNode(Parent *BTNode, Nodes []*Node, Childs []*BTNode) *BTNode { btNode := &BTNode{0, nil, nil, nil} btNode.Parent = Parent btNode.Nodes = make([]*Node, tree.M) //这里没有用链表实现 直接按照最大容量生成了 会有一定空间浪费 btNode.Childs = make([]*BTNode, tree.M+1) //这里没有用链表实现 直接按照最大容量生成了 会有一定空间浪费 if Nodes != nil { copy(btNode.Nodes, Nodes) btNode.KeyNum = len(Nodes) } if Childs != nil { copy(btNode.Childs, Childs) } return btNode } ```

删除操作简易介绍

删除操作相对麻烦一些，大概如下几个步骤：

  1. 首先找到key在树中的位置，包括树节点位置和树节点中key关键字数组中对应的下标，如果找不到自然返回删除失败

  2. 如果当前key在的节点不是叶子节点，则找到其后继key，用后继key覆盖要删除的key 然后删除后继key(肯定在叶子节点) 然后继续执行下面步骤

  3. 如果删除key所在节点是叶子节点 并且关键字数量删除后依然符合最小要求，则直接删除返回，结束。

  4. 如果删除key所在节点是叶子节点 但是关键字数量删除后不符合最小要求 做以下处理:

    4.1. 如果删除key所在节点的左右兄弟节点关键字数量个数都>最小要求个数，也就是可以从兄弟节点中借一个key过来，这样删除后关键字数量就都符合要求了，这里也牵扯到父节点中key的变化调整，相当于一次简单的旋转操作，下面有例子，至于左右兄弟节点如果都符合要求，从哪里借的问题，我个人选择的是关键字数量最大的兄弟节点

    4.2. 如果删除key所在节点的左右兄弟关键词数量都不符合要求(<=最小要求个数)，这时候需要将父节点中一个key下移，与其兄弟节点中的key合并成为一个新的节点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，然后从第3步开始重复判断操作，因为父节点下移一个节点，有可能关键字数量也不符合要求了，也要调整。

网搜简易删除图解m=5

  1. 删除前原始状态

  1. 删除21

    是叶子节点，并且删除后关键字数量符合最小要求(最小为2) 所以直接删除即可，注意修改该节点关键字数量，删除后为：

  2. 继续删除27

    非叶子节点，找到其后继key，也就是28，用后继key的值覆盖原先的key27，然后删除key变为key28（要删除图中28 29节点中的key28）删除后的样子如下：

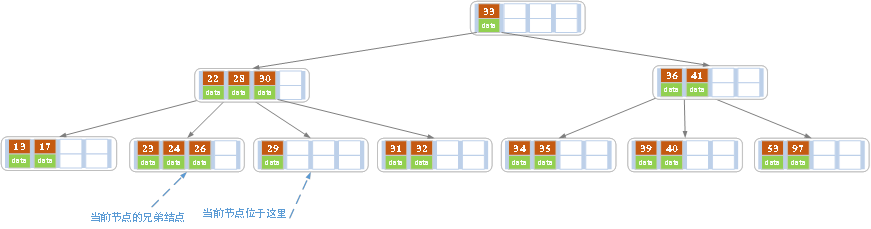
    这时候变成了情况4.1 有兄弟节点可以借关键字，所以父节点中的key28下移，兄弟节点中的key26节点顶替父亲节点中的key28位置，有点像对key28做一次右旋操作，但不完全相同。最后变为：

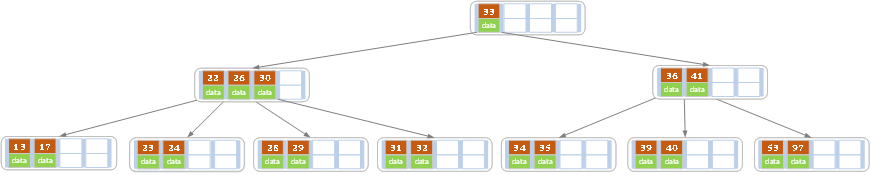
  3. 继续删除32

    删除32后，关键字不符合要求，而且兄弟节点也不能借，所以为情况4.2.

    这个时候合并兄弟节点 key31 跑到兄弟节点中(key28,key29所在节点)，同时让父节点中key30下移，跟其合并后新的孩子节点(key28,29,31)再次合并 同时注意修改父节点中的孩子指针。

    然后将当前节点指针改为父亲节点(key 22 26) 发现关键词数量符合要求，结束调整，最后为：

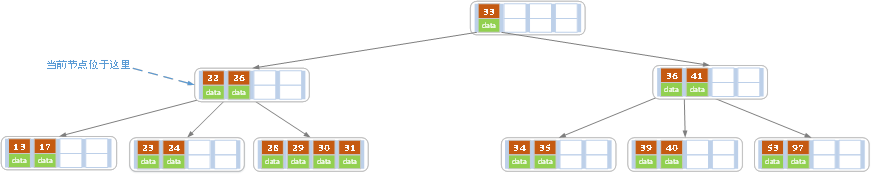
  4. 继续删除40

    属于情况4.2,删除后关键词不够了，兄弟节点也都不够借，key39–>(key34,35)—>(key 34,35,39)

    然后父节点的key36下移 变为(key 34,35,36,39) 指针指向其父节点

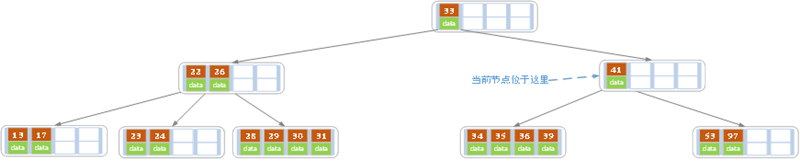
    然后发现还是情况4.2. Key41–>(key22,26)—>(key 22 26 41)

    然后父节点下移 变为(key22 26 33 41) 这个时候也不要忘记修改root指针

删除代码

BTree删除代码go版本 ```go //Delete 删除树中的key对应的数据对 返回删除成功或者失败 func (tree *BTree) Delete(Key interface{}) bool { flag, KeyDelIndex, delBtNode := tree.Search(Key) if flag == false || KeyDelIndex == -1 || delBtNode == nil { //找不到节点 return false } if tree.isLeafBtNode(delBtNode) == false { //非叶子节点 一定有左右孩子,找到删除Key的后继Key 也就是右孩子的最左孩子的第一个key successorBtNode := tree.getSuccessor(delBtNode, KeyDelIndex) fmt.Println(Key, "不是叶子节点，其后继key为:", successorBtNode.Nodes[0].Key) successorKeyNode := successorBtNode.Nodes[0] delBtNode.Nodes[KeyDelIndex] = successorKeyNode //用后继key覆盖原先要删除的key delBtNode, KeyDelIndex = successorBtNode, 0 //删除节点改为其后继bt节点 对应的KeyIndex就是其后继Key也就是0 此时后继节点肯定是叶子节点 } fmt.Println("删除节点Key:", delBtNode.Nodes[KeyDelIndex].Key, " 为叶子节点") //下面都是叶子节点的逻辑 先删除对应的Key 然后判断关键字数量 // key1--key2...KeyDelIndex.... KeyDelIndex后面的元素全部前移 然后该节点的关键字数量减1 for i := KeyDelIndex; i < delBtNode.KeyNum; i++ { delBtNode.Nodes[i] = delBtNode.Nodes[i+1] } delBtNode.KeyNum-- for delBtNode.KeyNum < tree.minKeyNum { //如果被删除叶子节点的关键字数量不符合要求 则需要调整 //先找到该节点的左右兄弟 尝试充兄弟中借key leftBroBtNode, rightBroBtNode, lBroIndexInPChilds, rBroIndexInPChilds := tree.getBrothers(delBtNode) if tree.borrowKeyFormBrothers(leftBroBtNode, rightBroBtNode, delBtNode, lBroIndexInPChilds, rBroIndexInPChilds) { //成功则返回 fmt.Println("兄弟节点够借") return true } fmt.Println("兄弟节点不够借 准备合并") //如果兄弟节点借不到 则需要合并节点了 delBtNode = tree.merge(delBtNode, leftBroBtNode, rightBroBtNode, lBroIndexInPChilds, rBroIndexInPChilds) if delBtNode.Nodes[0] != nil { fmt.Println("合并后删除节点变为其父节点 ", delBtNode.Nodes[0].Key) tree.PrintVisually() } } fmt.Println("删除完成") return true } //isLeafBtNode 检查一个节点是否是叶子节点 也就是没有孩子 func (tree *BTree) isLeafBtNode(btNode *BTNode) bool { if btNode == nil || btNode.KeyNum == 0 { return true } return btNode.Childs[0] == nil //如果是叶子节点 那么就没有一个孩子 第一个key的左孩子肯定为nil 否则就是非叶子节点 } //getSuccessor 传入某一个Bt节点和对应key的小标 找到该Key的后继Key 返回后继Key的Bt节点(当然后继Key肯定是该节点的第一个key) func (tree *BTree) getSuccessor(btNode *BTNode, index int) *BTNode { rightBtNode := btNode.Childs[index+1] retBtNode := rightBtNode for ; rightBtNode.Childs[0] != nil; retBtNode, rightBtNode = rightBtNode, rightBtNode.Childs[0] { //如果最左的孩子不为空 则继续往下找到最左的孩子 } return retBtNode } //getBrothers 传入一个bt节点 找到其左右兄弟返回 第一个返回值为左兄弟 同时也返回左右兄弟在父节点孩子节点指针数组中的下标 func (tree *BTree) getBrothers(btNode *BTNode) (*BTNode, *BTNode, int, int) { if btNode.Parent == nil { return nil, nil, -1, -1 } //遍历父节点重的孩子节点指针数组 找到该节点指针的下标，左边就是其左兄弟 右边就是其又兄弟 index := -1 var leftBroBtNode, rightBroBtNode *BTNode = nil, nil for i := 0; i <= btNode.Parent.KeyNum; i++ { if btNode.Parent.Childs[i] == btNode { index = i break } } if index == -1 { panic("在父亲节点中找不到该节点指针") } if index == 0 { //如果该节点是父亲节点的第一个孩子 则没有左兄弟 leftBroBtNode = nil } else { leftBroBtNode = btNode.Parent.Childs[index-1] } if index == btNode.Parent.KeyNum { //如果该节点是父亲节点的最后一个孩子 则没有右兄弟 rightBroBtNode = nil fmt.Println("没有右边兄弟 index=", index, "keyNum=", btNode.KeyNum) } else { rightBroBtNode = btNode.Parent.Childs[index+1] } return leftBroBtNode, rightBroBtNode, index - 1, index + 1 } //borrowKeyFormBrothers 从兄弟中借key 返回是否成功 //lBroIndexInPChilds, rBroIndexInPChilds 分别为左右兄弟在父节点孩子指针数组中的下标 func (tree *BTree) borrowKeyFormBrothers(leftBroBtNode *BTNode, rightBroBtNode *BTNode, delBtNode *BTNode, lBroIndexInPChilds int, rBroIndexInPChilds int) bool { //想从兄弟中借key首先本身兄弟key比较富足 否则返回失败，如果都比较富足，则取最富足的 //如果两者key数量相同 切都富足 则这里固定取左兄弟 if (leftBroBtNode == nil || leftBroBtNode.KeyNum <= tree.minKeyNum) && (rightBroBtNode == nil || rightBroBtNode.KeyNum <= tree.minKeyNum) { return false } isBorrowLeftBro, isBorrowRightBro := false, false //如果左兄弟为空或者左兄弟关键词数量小于右兄弟 则从右兄弟借 否则从左兄弟借 2兄弟key数量相等 也从左兄弟借 if leftBroBtNode == nil || leftBroBtNode.KeyNum < rightBroBtNode.KeyNum { isBorrowRightBro = true } else { isBorrowLeftBro = true } if isBorrowLeftBro { //从左兄弟借 //将父节点中对应key插入delBtNode中 插入到最左边 因为从父节点找到的key是大于左兄弟中的最大值 小于删除节点中的最小值的 for i := delBtNode.KeyNum; i > 0; i-- { delBtNode.Nodes[i] = delBtNode.Nodes[i-1] //原先节点全部后移一位 把最左边位置腾出来 } delBtNode.Nodes[0] = leftBroBtNode.Parent.Nodes[lBroIndexInPChilds] //父节点下来一个节点 delBtNode.KeyNum++ //将左兄弟中最靠右的key，也就是最大的key 插入到父节点换到被删除节点的key位置 leftBroBtNode.Parent.Nodes[lBroIndexInPChilds] = leftBroBtNode.Nodes[leftBroBtNode.KeyNum-1] leftBroBtNode.Nodes[leftBroBtNode.KeyNum-1] = nil leftBroBtNode.KeyNum-- return true } if isBorrowRightBro { //从右兄弟借 //将父节点中对应key插入delBtNode中 插入到最右边 因为从父节点找到的key左孩子指向是被删除的节点 大于删除节点中的最大值的 delBtNode.Nodes[delBtNode.KeyNum] = rightBroBtNode.Parent.Nodes[rBroIndexInPChilds] delBtNode.KeyNum++ //将右兄弟中最靠左的key，也就是最小的key 插入到父节点换到被删除节点的key位置 rightBroBtNode.Parent.Nodes[rBroIndexInPChilds] = rightBroBtNode.Nodes[0] //右兄弟中所有key元素前移一个位置 并将原先最后一个key的指针置空 for i := 0; i < rightBroBtNode.KeyNum; i++ { rightBroBtNode.Nodes[i] = rightBroBtNode.Nodes[i+1] } rightBroBtNode.Nodes[rightBroBtNode.KeyNum] = nil rightBroBtNode.KeyNum-- return true } return false } //merge 合并节点 将要删除的节点合并到传入的左/右兄弟节点中 返回其父节点 func (tree *BTree) merge(delBtNode *BTNode, leftBroBtNode *BTNode, rightBroBtNode *BTNode, lBroIndexInPChilds int, rBroIndexInPChilds int) *BTNode { if leftBroBtNode != nil { fmt.Println("传入左兄弟不为空") } if leftBroBtNode != nil { //只要左边兄弟不为nil 就将delBtNode合并到左兄弟节点中 //先将父节点中指向左兄弟的key也移动到左边兄弟中 leftBroBtNode.Nodes[leftBroBtNode.KeyNum] = leftBroBtNode.Parent.Nodes[lBroIndexInPChilds] leftBroBtNode.KeyNum++ //将delBtNode中的key全部移动到leftBroBtNode中 for i := 0; i < delBtNode.KeyNum; i++ { leftBroBtNode.Nodes[leftBroBtNode.KeyNum] = delBtNode.Nodes[i] leftBroBtNode.Childs[leftBroBtNode.KeyNum] = delBtNode.Childs[i] leftBroBtNode.KeyNum++ } leftBroBtNode.Childs[leftBroBtNode.KeyNum] = delBtNode.Childs[delBtNode.KeyNum] //处理父节点的key数组和孩子指针数组 因为delBtNode合并到左兄弟中了 所以原先父节点指向delBtNode的指针就要删除了 //key数组因为有一个放到删除节点的左兄弟中 所以其右的所有key往前移动一个 for i := lBroIndexInPChilds; i < leftBroBtNode.Parent.KeyNum; i++ { leftBroBtNode.Parent.Nodes[i] = leftBroBtNode.Parent.Nodes[i+1] } //因为delBtNode合并到左兄弟节点中了 所以父节点中孩子指针数组 delBtNode后边的全部往前移动一位 for i := lBroIndexInPChilds + 1; i <= leftBroBtNode.Parent.KeyNum; i++ { leftBroBtNode.Parent.Childs[i] = leftBroBtNode.Parent.Childs[i+1] } leftBroBtNode.Parent.KeyNum-- if leftBroBtNode.Parent == tree.Root { tree.Root = leftBroBtNode return leftBroBtNode } return leftBroBtNode.Parent } //没有左兄弟节点 合并到右兄弟节点 其中父亲节点中指向左兄弟节点的key也转移到右兄弟节点 //新申请一个slice 先后将delBtNode、父节点、右兄弟的key复制进去 newNodes := make([]*Node, tree.M) i := 0 for ; i < delBtNode.KeyNum; i++ { newNodes[i] = delBtNode.Nodes[i] } //将父节点元素也复制到右兄弟节点 newNodes[i] = rightBroBtNode.Parent.Nodes[rBroIndexInPChilds-1] i++ //将原先兄兄弟中的节点也copy到新申请的slice for j := 0; j < rightBroBtNode.KeyNum; i, j = i+1, j+1 { newNodes[i] = rightBroBtNode.Nodes[j] } rightBroBtNode.Nodes, rightBroBtNode.KeyNum = newNodes, i //新申请一个slice 存放合并后的孩子指针 newChilds := make([]*BTNode, tree.M+1) //先后将delBtNode和rightBroBtNode的孩子指针cp进来 j := 0 for ; j <= delBtNode.KeyNum; j++ { newChilds[j] = delBtNode.Childs[j] } for k := 0; k <= rightBroBtNode.KeyNum; j, k = j+1, k+1 { newChilds[j] = rightBroBtNode.Childs[k] } rightBroBtNode.Childs = newChilds //处理父节点的key数组和孩子节点数组 //有一个key去了右兄弟节点 所以这个key后面的所有key都要前移 for i := rBroIndexInPChilds - 1; i < rightBroBtNode.Parent.KeyNum; i++ { rightBroBtNode.Parent.Nodes[i] = rightBroBtNode.Parent.Nodes[i+1] } //处理孩子指针数组 for i := rBroIndexInPChilds - 1; i <= rightBroBtNode.Parent.KeyNum; i++ { rightBroBtNode.Parent.Childs[i] = rightBroBtNode.Parent.Childs[i+1] } rightBroBtNode.KeyNum-- return rightBroBtNode.Parent } ```

B+树

待补充

Hash

一些哈希函数的性质

  • input一般无穷

  • output有限范围

  • 同样的input 同样的output

  • 因为input无穷 output有限 必定出现不同的input 同样的output情况 hash碰撞或者hash冲突

  • 大量不同的input 经过hash函数后 output上大致均匀分布 也就是hash函数的离散型

    如果hashcode在output域均匀分布，那么每个hashcode%M,也就是对M取模后 则在0到M-1的范围也是均匀分布的

制造hash函数

思路

  • 假设手上有1个比较不错的hash函数，针对每一个hashcode 都将其内存一分为二，也就是对于一个Hashcode将其拆分为h1和h2 各占一半字节
  • 然后h1+1*h2 就是一个新的hash算法
  • 同理h1+2*h2也是一个新的hash算法 而且彼此独立。可以改变系数 得到大量的hash函数

当然也可以准备2个hash函数 结果对应分别为h1 h2 按照同样的思想来回组合即可

hashcode的每一位根其它的位都是独立的 互不相关的，所以这么组合来的就也不相关。

hash表相关

​ hash表也就是存放hashcode和数据(数据地址)的地方，hash表通常可以是单链表实现(相同的hashcode用链表链接存放)，Java的是用红黑树，避免了重复扩容带来的代价。

一些hash应用

1 统计大文件中的重复的行

  • 如果文件太大，比如100T，单台机器是搞不定的(时间太长)
  • 分布式多台机器解决，假设有1000台机器，分布式并发读取每一行，经过同样的hash函数得到hashcode然后对1000取模，分到不同的机器，这样以来就把100T文件大致均匀的分到了1000个机器上面，而且相同的行一定分到了同一台机器上。
  • 然后1000台 每个机器也可以再经过一个hash 扔给不同的线程并发计算 最后综合下结果。

利用了相同输入 相同输出，大量不同输入，结果均匀分布的性质，将大任务搞成小任务，小任务可以继续再小任务。

设计一个randomePool

题目描述

设计RandomPool结构 【题目】 设计一种结构，在该结构中有如下三个功能: insert(key):将某个key加入到该结构，做到不重复加入。 delete(key):将原本在结构中的某个key移除。 getRandom(): 等概率随机返回结构中的任何一个key。 【要求】 Insert、delete和getRandom方法的时间复杂度都是 O(1)

思路：

  1. 准备2个hashmap。hash1key:value=<元素值:存放次序编号从0开始 >，hash2key:value=<存放次序编号:元素值>

  2. 添加的时候2个hashmap都加入，存放次序编号+1

  3. get的时候需要随机就比较简单了 因为从0到N顺序放入的元素及次序都在hash2中了 生成一个从0—>N的随机数 然后作为key从hash2中拿到其元素值即可

  4. 删除的时候需要注意 不能直接删除，比如删除了编号为10的元素，在hash2中编号为10的的位置就空了出来，如果随机出来编号10，则会出现问题，所以需要将最后一个元素覆盖编号为10的元素，同时删除最后一个元素，这样元素都还是顺序存放的，编号不会出现空洞，也成功实现了删除， removeIndex为删除元素的编号，removeValue为要删除的元素，size为删除前总元素个数，这个时候删除的大值逻辑如下：

    lastValue=delete(hash2<size-1>);//从hash2删除最后一个元素 
delete(hash1<lastValue>);//从hash1删除最后一个元素
hash2<removeIndex>=lastValue;//hash2中用最后一个元素覆盖removeIndex原先的值 实现删除
delete(hash1<removeValue>);//从hash1中删除要删除的元素
hash1<removeIndex>=lastValue;//hash1用最后元素的值覆盖原先要删除的元素
size--; 整体数量减1

代码

转载JAVA ```Java public class Code_02_RandomPool { public static class Pool { private HashMap keyIndexMap; private HashMap indexKeyMap; private int size; public Pool() { this.keyIndexMap = new HashMap(); this.indexKeyMap = new HashMap(); this.size = 0; } public void insert(K key) { if (!this.keyIndexMap.containsKey(key)) { this.keyIndexMap.put(key, this.size); this.indexKeyMap.put(this.size++, key); } } public void delete(K key) { if (this.keyIndexMap.containsKey(key)) { int deleteIndex = this.keyIndexMap.get(key); int lastIndex = --this.size; K lastKey = this.indexKeyMap.get(lastIndex); this.keyIndexMap.put(lastKey, deleteIndex); this.indexKeyMap.put(deleteIndex, lastKey); this.keyIndexMap.remove(key); this.indexKeyMap.remove(lastIndex); } } public K getRandom() { if (this.size == 0) { return null; } int randomIndex = (int) (Math.random() * this.size); // 0 ~ size -1 return this.indexKeyMap.get(randomIndex); } } public static void main(String[] args) { Pool pool = new Pool(); pool.insert("zuo"); pool.insert("cheng"); pool.insert("yun"); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); System.out.println(pool.getRandom()); } } ```
### 大数量黑名单查询

题目描述

  • 假设有100亿条黑名单url，设计一个黑名单查询服务
  • 每个url大概64字节，不算其它成本 但url字节存储到内存大概需要640G

思路

  • 全部存储到单机器内存，用不同的set实现，缺点很明显 单台机器很难有这么多内存，而且成本太高
  • 通过hash，将640G内存对应的100亿条黑名单url 大值均匀分布到1000台机器，然后通过rpc通信让1000台机器一起来抗，可以实现，不过成本较高，需要大量的机器
  • 布隆过滤器 大大降低内存使用，同时单台机器即可提供服务，缺点有一定的失误率(非黑名单也会判定会黑名单)，如果可以接受一定的失误率 布隆过滤器应该是最优选择

布隆过滤器

  • 既然要降低内存使用，最简单的思路就是准备比特bit类型的数组，让每一个bit都能代表相应的含义，这样就最大化的利用内存

  • 如何让每一位bit都能代表相应的含义 ：

    假设准备一个M长度的bit类型数组，我们让一个url经过一个hash算法，得到hashcode，然后让这个hashcode对M取模 得到下标index，将bit数组下标为index的位置置为1 ，查找url的时候也是同样的逻辑，经过hash算法得到hashcode，然后对M取模得到下标，然后查看下标为index的位置元素值是否为1。通过这样的hash转换我们就让这个bit数组有了实际含义

  • 布隆过滤器 针对不同的失误率要求 往往会准备多个hash，相对更大的bit数组：

    关于多个hash：多个hash主要是为了降低hash冲突的概率 只有多个hash对M取模后都是1 才说明是黑名单，只要有一个不是则说明没有进过。

    关于bit数组长度：如果数组长度太短，大量url经过hash和取模后 全部数组都变为了1 那么就全是黑名单了 显然不符合要求。

  • M= - (N * lnP) / ( (ln2)^2 ) N为样本量 P为失误率 算出的M为bit类型的长度。100亿数据 失误率万分之一 大概M为16G

  • hash函数个数选择 K= ln2 *(M/N) K为hash个数

  • M K向上取整后 真实失误率P= (1- E(-N*K/M))

一定不存在、可能存在、不能删除

如果经过多个hash对应的bit位如果有一个不是1 则说明一定不在这个集合中(因为如果进过集合 则对应的位置应该全都是1)，否则说明可能存在这个集合，关于可能存在举个例子。

假设X进行三次hash后对应的bit位是**(0,3,6)**

Y被三次hash后对应的bit位是**(0,3,7)**，则Y在bit的0和3的值会覆盖掉X的值，

假设还有一个新元素Z的hash结果是**(1,3,6)，则意味着X的hash结果被全部覆盖，也就是说即使没有X，(0,3,6)位置的值也是1**，所以只能是有可能存在。

也正是因为这种情况 删除的X的时候 不能将对应bit为全部只为0 这样的Y，Z也被剔除集合了。

几种优化

CBF Counting Bloom Filter，为了支持删除，把原先的每个bit位改为对应的每个counter，每次hash对应的值+1 空间有所增加，有所浪费

SBF（Spectral Bloom Filter）在 CBF 的基础上提出了元素出现频率查询的概念，将CBF的应用扩展到了 multi-set 的领域；

dlCBF（d-Left Counting Bloom Filter）利用 d-left hashing 的方法存储 fingerprint，解决哈希表的负载平衡问题；

ACBF（Accurate Counting Bloom Filter）通过 offset indexing 的方式将 Counter 数组划分成多个层级，来降低误判率

布隆过滤器的其它一些应用：

​ 假设：redis当前放的热点数据，黑客高频非法id数据来查询，就可能出现问题(redis查不到 直接查数据库，那么数据库压力山大；如果查询不到直接将结果全部缓存的redis，那么redis内存压力大，而且这些是非法数据，redis内存淘汰策略可能吧正常的热点数据淘汰掉)。

如果在redis热点和数据库中间加一个布隆过滤器可能会比较快

  1. redis热点找不到 再看布隆过滤器在不在，如果不在直接返回client（非法请求）
  2. 如果布隆过滤器存在 则去数据库查询(虽然可能存在其实不存在的问题，因为布隆过滤器有一定的失误率，但这个一般比较小) 这样就很大可能地方黑客的攻击

一致性哈希算法基本原理

题目:

服务器集群来设计和实现数据缓存–常见的策略：

  1. 无论是添加、查询还是删除数据，都先将数据的id通过哈希函数换成一个哈希值，记为key
  2. 如果目前机器有N台，则计算key%N的值，这个值就是该数据所属的机器编号，无论是添加、删除还是查询操作，都只在这台机器上进行。

这样来实现集群的负载均衡 这个跟经典负载均衡算法中的源IP算法有点类似

上述经典hash负载均衡算法 存在什么问题

  1. 如果增加或者删除机器 代表会变得很高，因为原先都是对N取模的，现在要变为对N+1台机器编号取模，之前的所有hash计算都要重新计算 这个代码是比较高的，其实跟hash扩容有点类似

一致性算法原理大值描述

我们假设hashcode的范围为0—>2^32 ，将其范围想象为一个环

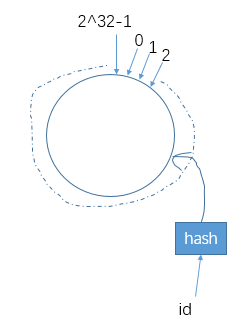
接下来我们对应不同的机器，根据其特质(假设三台机器 根据其id)，针对其id用hash函数 计算出其hashcode，对应在环上，大致如下:

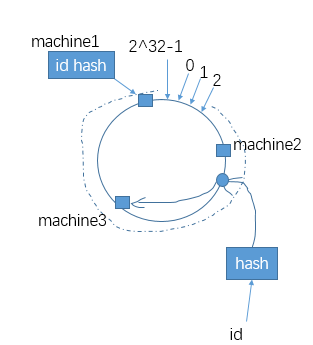
​ 现在对于所有input，经过同样的hash函数计算出的hashcode，打到环上，顺时针往前找到的第一个机器idhash就是其要存放的机器，实现上可以将所有机器id的hash值放到排好序的数组，然后使用的时候二分查找第一个>=其hashcode的机器id hashcode即可

这个时候如果删除节点m2 则将m2机器上的所有数据转移到m3即可，不用把所有数据都全部再hash一次。

但这样又回引入一个问题，因为这种算法跟经典的少了取模运算，所以分到各个机器上的数量很有可能是不均衡的。

增加删除机器也可能导致不均衡。

为了解决这个问题，就引入了虚拟节点技术。即对每一台机器通过不同的哈希函数计算出多个哈希值，对多个位置都放置一个服务节点，称为虚拟节点。具体做法：比如对于machine1的IP192.168.25.132（或机器名），计算出192.168.25.132-1、192.168.25.132-2、192.168.25.132-3…..192.168.25.132-1000的哈希值，然后对应到环上，其他的机器也是如此，这样的话节点数就变多了，根据哈希函数的性质，平衡性自然会变好：

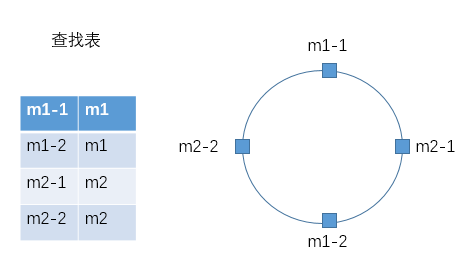
引入虚拟节点需要实现一张路由表，要知道机器对应的所有虚拟节点值，根据虚拟节点值也要很快找到对应的机器，而且要注意增加删除节点的时候要根据虚拟节点值先来计算 再对应到所属的机器上进行迁移。

基于一致性哈希的原理有很多种具体的实现，包括Chord算法、KAD算法等，后续再进一步学习

并查集

定义

并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

  • Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
  • Union：将两个子集合并成同一个集合。

实现

初始化

并查集不适用流结构，也就是不能动态变化，只能在一开始直接初始化好，刚开始的时候一个元素构成一个节点 并且父节点指向自身

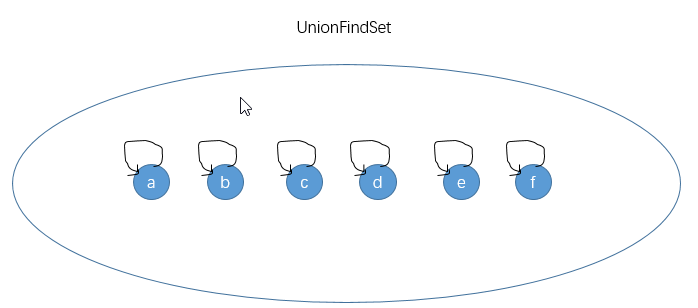
合并

可以对任意两个元素进行合并操作。值得注意的是，union(nodeA,nodeB)并不是将结点nodeA和nodeB合并成一个集合，而是将nodeA所在的集合和nodeB所在的集合合并成一个新的子集，大值图解如下:

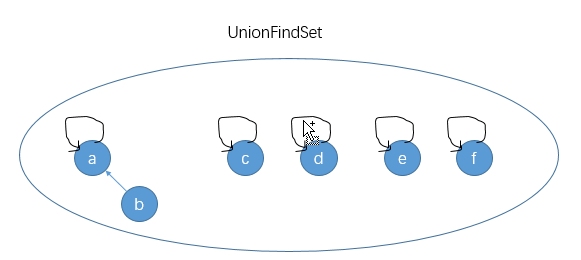
代表节点：就是一个集合中谁的父节点指向自己，强行规定，刚开始ab节点独立，2个集合，代表节点都是自身，然后合并ab节点

现在ab节点在一个集合，代表节点就是a，因为其父节点指向自身，一般合并的时候将集合节点数小的集合直接合并到节点数大的集合中，合并操作其实也就是将size小的集合的代表节点的父节点指针改为节点数大的集合的代表节点，相同size大小 随意

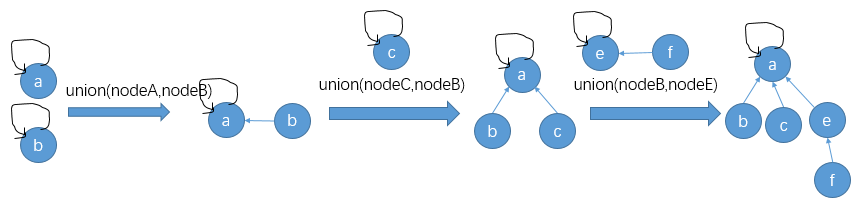
查找

查询2个节点是否在同一个集合，也就是网上找到它的代表节点 看是否同一个，同时在查找的过程中，该元素到代表节点上的所有节点的父节点都直接改为代表节点，这样以来下次再查找的时候效率就更好了，只需查找1次就搞定了。

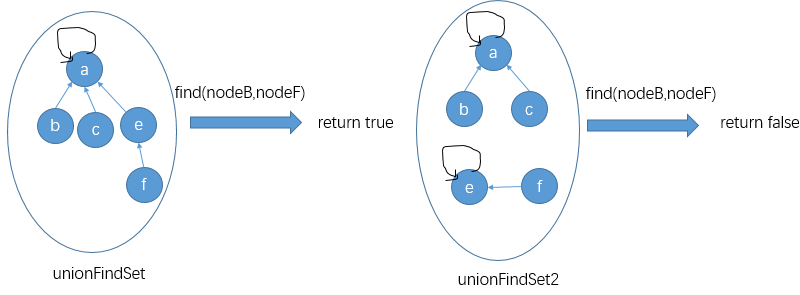
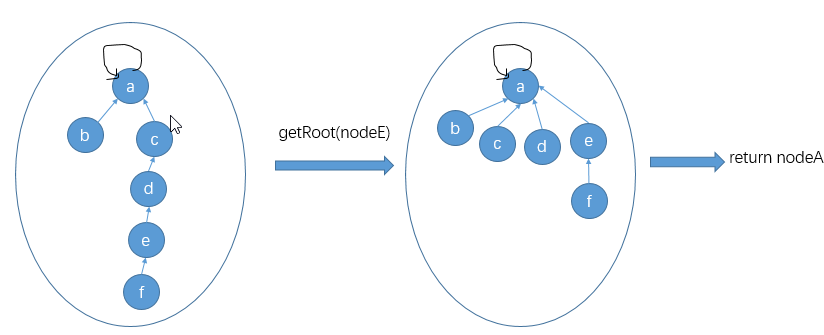
代码实现

​ 可以用2个hashmap实现：

  1. fartherMap<节点,对应父节点>
  2. sizeMap<代表节点,集合节点个数>
  3. 刚开始加入farther每个节点都入hash，父节点都指向自己，sizemap代表节点就是自己，元素个数为1
  4. 合并的时候 注意修改被合并集合代表节点的父节点指针 同时修改合并后集合代表集合对应的集合个数即可
  5. 查找的时候注意将被被查找元素网上的所有非代表节点的父节点都直接指向代表节点，提高下次查找效率
转载java 自己实现也很简单 ```Java public static class Node { // whatever you like } public static class UnionFindSet { public HashMap fatherMap; public HashMap sizeMap; public UnionFindSet() { fatherMap = new HashMap(); sizeMap = new HashMap(); } public void makeSets(List nodes) { fatherMap.clear(); sizeMap.clear(); for (Node node : nodes) { fatherMap.put(node, node); sizeMap.put(node, 1); } } private Node findHead(Node node) { Node father = fatherMap.get(node); if (father != node) { father = findHead(father); } fatherMap.put(node, father); return father; } public boolean isSameSet(Node a, Node b) { return findHead(a) == findHead(b); } public void union(Node a, Node b) { if (a == null || b == null) { return; } Node aHead = findHead(a); Node bHead = findHead(b); if (aHead != bHead) { int aSetSize= sizeMap.get(aHead); int bSetSize = sizeMap.get(bHead); if (aSetSize <= bSetSize) { fatherMap.put(aHead, bHead); sizeMap.put(bHead, aSetSize + bSetSize); } else { fatherMap.put(bHead, aHead); sizeMap.put(aHead, aSetSize + bSetSize); } } } } ```

前缀树

相关介绍

前缀树是一种存储字符串的高效容器，基于此结构的操作有：

  • insert插入一个字符串到容器中
  • search容器中是否存在某字符串，返回该字符串进入到容器的次数，没有则返回0
  • delete将某个字符串进入到容器的次数减1
  • prefixNumber返回所有插入操作中，以某个串为前缀的字符串出现的次数

设计思路：该结构的重点实现在于存储。前缀树以字符为存储单位，将其存储在结点之间的树枝上而非结点上，如插入字符串abc之后前缀树如下：

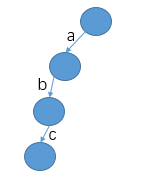
insert操作逻辑：

​ 每次插入字符串，将字符串改为字符数组，逐个遍历，看看树头是否有岛该字符的路径，如果有树的指针往下走，然后对下一个字符执行相同的操作，比如插入"abc"，发现存在abc的路径，不新增节点，只是将到达该节点的次数+1,同时以c结尾的次数+1.

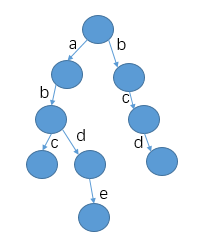
如果插入"abde" 则ab2个字符不用新增节点 因为不存爱b–>d的路 所以需要新增节点

节点保存的时候需要额外保存2个信息(到达该字符的次数 path，以该字符结尾的字符串个数 endNum)

查找“abc”字符串出现的次数

1. 前缀树是否有a的路径 有则继续 没有返回0
  	2. a有没有指向b的路径 有则继续 没有返回0
     	3. b有没有指向c的路径  没有返回0，有则返回以c为结束字符的个数 endNUm

查找以"ab"打头的字符串的个数

  1. 前缀树是否有到a的路径，有则继续 没有返回0
  2. 是否有a到b的路径 没有返回0，有则返回到b的路径次数 path

删除逻辑

比如删除字符串abc

  1. 首先字符串"abc"出现的次数是否>0 如果没有出现过 则直接返回，否则继续
  2. 找到指向a的路径，对应path– 如果path减后变为0 则说明以a打头的只有一个abc 直接将指向a的路径置空返回 c++注意释放内存
  3. 找到指向b的路径 对应path– 如果path减后变为0 则说明以ab打头的只有一个abc 直接将指向b的路径置空返回 c++注意释放内存
  4. 找到指向c的路径 对应path– endNum– 如果path减后变为0 则说明以ab打头的只有一个abc 直接将指向c的路径置空返回 c++注意释放内存

代码实现

转载JAVA ```JAVA package class_07; public class Code_01_TrieTree { public static class TrieNode { public int path; public int end; public TrieNode[] nexts; public TrieNode() { path = 0; end = 0; nexts = new TrieNode[26]; } } public static class Trie { private TrieNode root; public Trie() { root = new TrieNode(); } public void insert(String word) { if (word == null) { return; } char[] chs = word.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (node.nexts[index] == null) { node.nexts[index] = new TrieNode(); } node = node.nexts[index]; node.path++; } node.end++; } public void delete(String word) { if (search(word) != 0) { char[] chs = word.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (--node.nexts[index].path == 0) { node.nexts[index] = null; return; } node = node.nexts[index]; } node.end--; } } public int search(String word) { if (word == null) { return 0; } char[] chs = word.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (node.nexts[index] == null) { return 0; } node = node.nexts[index]; } return node.end; } public int prefixNumber(String pre) { if (pre == null) { return 0; } char[] chs = pre.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (node.nexts[index] == null) { return 0; } node = node.nexts[index]; } return node.path; } } public static void main(String[] args) { Trie trie = new Trie(); System.out.println(trie.search("zuo")); trie.insert("zuo"); System.out.println(trie.search("zuo")); trie.delete("zuo"); System.out.println(trie.search("zuo")); trie.insert("zuo"); trie.insert("zuo"); trie.delete("zuo"); System.out.println(trie.search("zuo")); trie.delete("zuo"); System.out.println(trie.search("zuo")); trie.insert("zuoa"); trie.insert("zuoac"); trie.insert("zuoab"); trie.insert("zuoad"); trie.delete("zuoa"); System.out.println(trie.search("zuoa")); System.out.println(trie.prefixNumber("zuo")); } } ```

经典题目

一个字符串类型的数组arr1，另一个字符串类型的数组arr2：

  • arr2中有哪些字符，是arr1中出现的？请打印
  • arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印
  • arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印arr2中出现次数最大的前缀

将2个数组遍历构建一个前缀树，后面的判断利用前缀树实现。

动态规划

暴力递归与动态规划的关系

​ 暴力递归：

  1. 把问题转化为规模缩小了的同类问题的子问题
  2. 有明确的不需要继续进行递归的条件(base case)
  3. 有当得到了子问题的结果之后的决策过程
  4. 不记录每一个子问题的解

动态规划：

  1. 从暴力递归中来

  2. 将每一个子问题的解记录下来，避免重复计算

  3. 把暴力递归的过程，抽象成了状态表达

  4. 并且存在化简状态表达，使其更加简洁的可能

动态规划由暴力递归而来，是对暴力递归中的重复计算的一个优化，策略是空间换时间

暴力递归存在重复计算的状态，而且这些状态跟从什么位置到来这个地方没有关系(无后效性问题)，都可以改为动态规划。

求N！N的阶乘问题

暴力递归

  1. 如果知道N-1的阶乘 那么就知道了N!=N*f(N-1)
  2. basecase为 当N为1时候 f(1)=1 不需要再次递归
  3. 当知道f(N-1)就知道了f(N)

递归代码

int getFactorial(int N){
	if( N==1){//base case 不用再递归了
		return 1;
	}
	return N*getFactorial(N-1);
}

优化暴力递归

  • 知道了f(1)=1 就知道了f(2)=2 * f(1)=1 * 2 就知道了f(3)=3 * f(2)=1 * 2 * 3 也就可以直接计算了
int getFactorial_1(int N){
	int res=1;
	for(int i=1;i<=N;++i){
		res*=i;
	}
	return res;
}

汉诺塔问题

题目描述

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

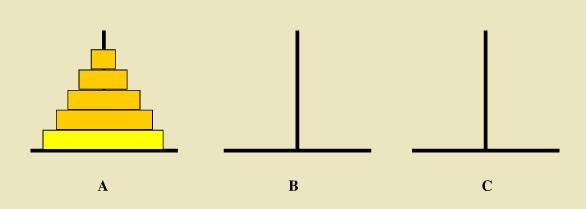
递归思路

  1. 假设有N都在A上 递归步骤如下:

    1.1 首先肯定是将上面的N-1 移动到B(辅助)，

    1.2 然后将A只剩下的一个 直接移动到C

    1.3 然后将B上面的N-1移动到C 解决问题

  2. base case如果只剩下一个 直接移动到目标即可

//A就是from B就是help C就是to 返回移动次数
int hanoi(int N,string from,string help,string to){
	int count=0;//移动次数
	count+=hanoi(N-1,from,to,help);//首先肯定是将上面的N-1 移动到B 这个时候可以用C辅助
	cout<<N<<"从"<<from<<"移动到"<<to<<endl;//然后将A只剩下的一个 直接移动到C
	count++;//累计移动次数
	count+=haoni(N-1,help,from,to);//然后将B上面的N-1移动到C 解决问题
	return count;
}

最小路径和

给你一个二维数组，二维数组中的每个数都是正数，要求从左上角走到右下角，每一步只能向右或者向下。沿途经过的数字要累加起来。返回最小的路径和。

遇到类似题目，往往先写出一个最基础版本的递归，然后再考虑优化

暴力递归思路

只能往右或者往下，所以对于一个点P1(iBegin,jBegin)到另外一个点P2(iEnd,jEnd)的最小路径和就等于 min( F(P1.right),F(P1.Down) )+value(iBegin,jBegin),当然对于i,j有一些边界要处理，比如i到达了最下面的行，只能往右，j到达了最右边的列只能往下。

basecase也就是递归终止条件为 当 i == iEnd && j == jEnd,也就是到达了终点，返回终点坐标的value即可。

//转载Java
public static int minPathSum(int matrix[][], int i, int j) {
  // 如果(i,j)就是右下角的元素
  if (i == matrix.length - 1 && j == matrix[0].length - 1) {
    return matrix[i][j];
  }
  // 如果(i,j)在右边界上，只能向下走
  if (j == matrix[0].length - 1) {
    return matrix[i][j] + minPathSum(matrix, i + 1, j);
  }
  // 如果(i,j)在下边界上，只能向右走
  if (i == matrix.length - 1) {
    return matrix[i][j] + minPathSum(matrix, i, j + 1);
  }
  // 不是上述三种情况，那么(i,j)就有向下和向右两种决策，取决策结果最小的那个
  int left = minPathSum(matrix, i, j + 1);
  int down = minPathSum(matrix, i + 1, j);
  return matrix[i][j] + Math.min(left,down );
}
public static void main(String[] args) {
  int matrix[][] = { 
    { 9, 1, 0, 1 }, 
    { 4, 8, 1, 0 }, 
    { 1, 4, 2, 3 } 
  };
  System.out.println(minPathSum(matrix, 0, 0)); //14
}

这里假设为3*4的矩阵 从(0,0)走到(2,3) f(0,0)需要计算f(0,1)和f(1,0), f(1,0)需要**计算f(1,1)和f(2,0) f(0,1) 需要计算f(1,1)**和f(2,1),

暴力递归 f(1,1)会存在重复计算 所以就浪费时间，最简单的优化可以把f(1,1)计算前，先判断是否已经计算过了，计算过了就直接使用，

如果没有计算过，计算完后就记下来(比如 map<string,value> map[“1_1”]=xxx).

优化

​ 由暴力递归改为动态规划的核心就是将子步骤的计算结果保存下来，从而达到空间换时间的目的，那么minPath(int matrix[][],int i,int j)中变量i和j的不同取值将导致i*j种结果，我们将这些结果保存在一个i*j的表中，假设叫做DP，DP(i,j)就是坐标i,j到终点的最小路径和。

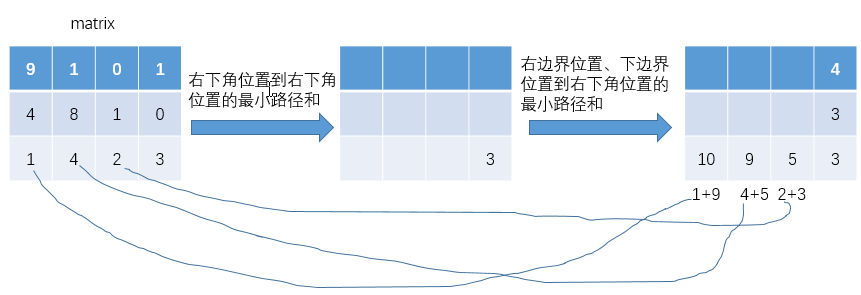
basecase为右下角的3，最后一行和最后一列其实可以直接从右往左，从下往上直接推出结果，接下来对于倒数第二行和倒数第二列也是同样的从右往左，从下往上直接推出结果。

​

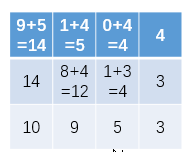
整个过程没有重复计算，所以动态规划问题就是优化暴力递归，所以首先要写出暴力递归版本，然后分析可变参数，看看那些返回值能够代表返回值的状态，可变参数是几纬的，状态结果表就是几纬的。 然后检查basecase，看看那些可以直接得到结果，对于一个普遍的状态看看它的依赖状态，然后按照相反的顺序推结果。

代码

动态规划求最小路径和 转载Java ```java package class_08; public class Code_07_MinPath { public static int minPath1(int[][] matrix) { return process1(matrix, matrix.length - 1, matrix[0].length - 1); } //递归版本 public static int process1(int[][] matrix, int i, int j) { int res = matrix[i][j]; if (i == 0 && j == 0) { return res; } if (i == 0 && j != 0) { return res + process1(matrix, i, j - 1); } if (i != 0 && j == 0) { return res + process1(matrix, i - 1, j); } return res + Math.min(process1(matrix, i, j - 1), process1(matrix, i - 1, j)); } public static int minPath2(int[][] m) { if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) { return 0; } int row = m.length; int col = m[0].length; int[][] dp = new int[row][col]; dp[0][0] = m[0][0]; for (int i = 1; i < row; i++) { dp[i][0] = dp[i - 1][0] + m[i][0]; } for (int j = 1; j < col; j++) { dp[0][j] = dp[0][j - 1] + m[0][j]; } for (int i = 1; i < row; i++) { for (int j = 1; j < col; j++) { dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j]; } } return dp[row - 1][col - 1]; } // for test public static int[][] generateRandomMatrix(int rowSize, int colSize) { if (rowSize < 0 || colSize < 0) { return null; } int[][] result = new int[rowSize][colSize]; for (int i = 0; i != result.length; i++) { for (int j = 0; j != result[0].length; j++) { result[i][j] = (int) (Math.random() * 10); } } return result; } public static void main(String[] args) { int[][] m = { { 1, 3, 5, 9 }, { 8, 1, 3, 4 }, { 5, 0, 6, 1 }, { 8, 8, 4, 0 } }; System.out.println(minPath1(m)); System.out.println(minPath2(m)); m = generateRandomMatrix(6, 7); System.out.println(minPath1(m)); System.out.println(minPath2(m)); } } ```

数组中任意数的和是否为Aim值

给你一个数组arr，和一个整数aim。如果可以任意选择arr中的数字，能不能累加得到aim，返回true或者false。

思路

​ 跟字符串的子序列类似，针对数组中的数只有2中状态，要或者不要，所以直接暴力递归

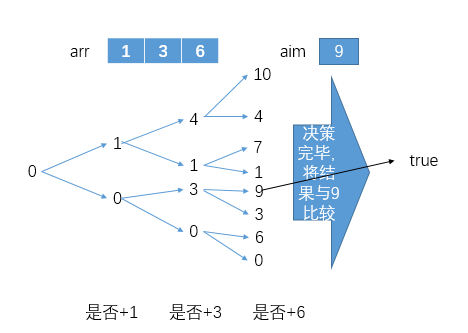
//转载java
//arr为原数组 aim为目标和 i，sum代表来到了下标为i的位置已经得到的sum值
public static boolean isSum(int arr[], int aim, int sum,int i) {
  //决策完毕
  if (i == arr.length) {//最后一个元素也已经判断完毕 就看sum是否有累计为aim的 
    return sum == aim;
  }
  //决策来到了arr[i]：加上arr[i]或不加上。将结果扔给下一级
  return isSum(arr, aim, sum + arr[i], i + 1) || isSum(arr, aim, sum, i + 1);
}

优化

​ 我们假设数组都是整数，分析函数的可变参数，只有sum和i可以变化，数组长度为N，i的变化范围就是N，

sum的变化范围是0—>所有数组元素之和。建立一个二维表，就拿数组[1,3,6] aim为9举例

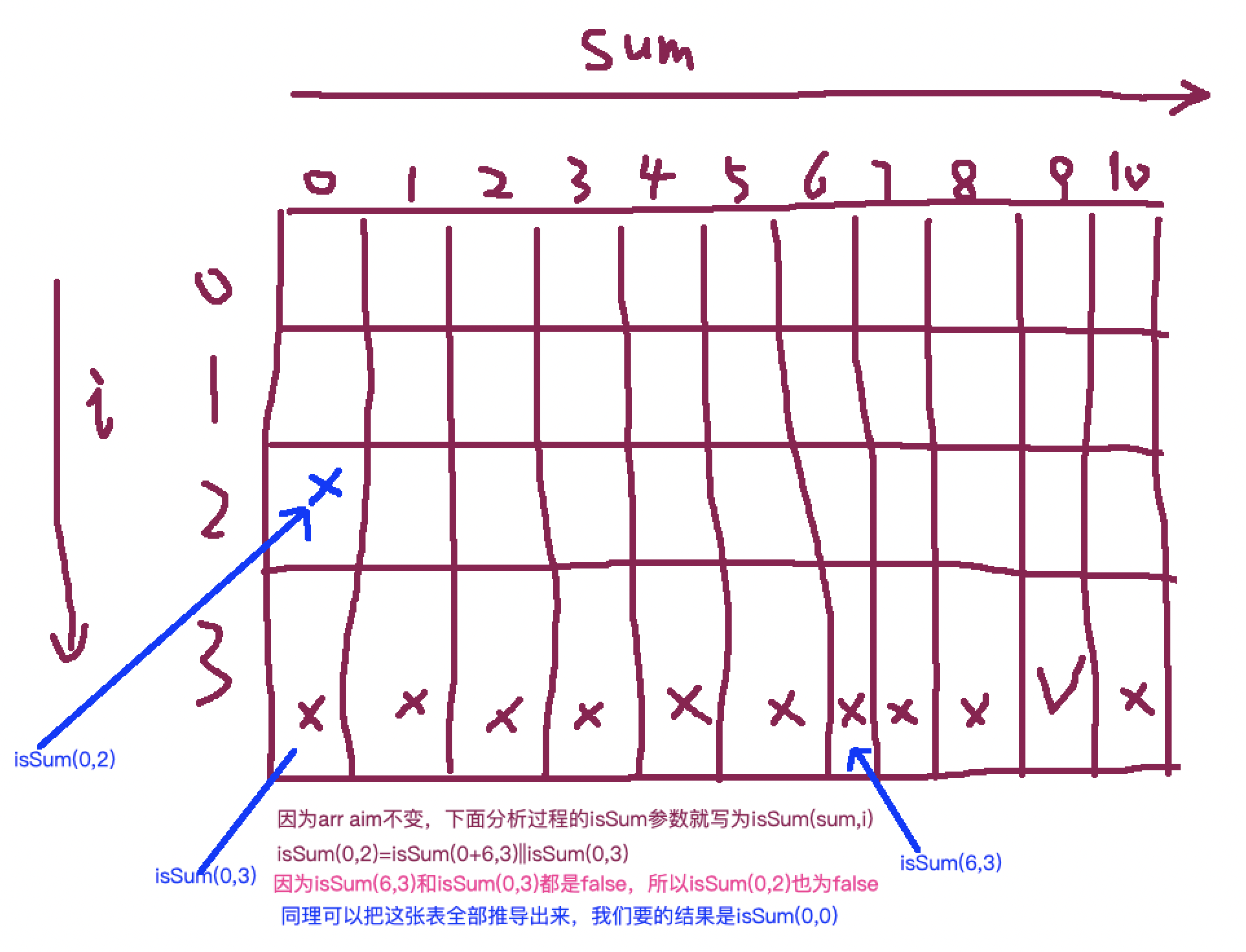
代码

动态规划求数组任意数和是否为aim 转载Java ```java package class_08; public class Code_08_Money_Problem { public static boolean money1(int[] arr, int aim) { return process1(arr, 0, 0, aim); } public static boolean process1(int[] arr, int i, int sum, int aim) { if (sum == aim) { return true; } // sum != aim if (i == arr.length) { return false; } return process1(arr, i + 1, sum, aim) || process1(arr, i + 1, sum + arr[i], aim); } public static boolean money2(int[] arr, int aim) { boolean[][] dp = new boolean[arr.length + 1][aim + 1]; for (int i = 0; i < dp.length; i++) { dp[i][aim] = true; } for (int i = arr.length - 1; i >= 0; i--) { for (int j = aim - 1; j >= 0; j--) { dp[i][j] = dp[i + 1][j]; if (j + arr[i] <= aim) { dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]]; } } } return dp[0][0]; } public static void main(String[] args) { int[] arr = { 1, 4, 8 }; int aim = 12; System.out.println(money1(arr, aim)); System.out.println(money2(arr, aim)); } } ```

背包问题

题目描述

一些算法题目

反转链表

题目描述

反转一个单链表。示例:

输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/reverse-linked-list 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解答1 双指针逐个反转2个节点

  1. 声明2个指针p1 p2,p1先指向NULL,p2指向head. p2永远在p1前面
  2. p2的next指向p1,然后p1,p2都向前走一步(当然要先记下来p2的next),直到p2为NULL
  3. 循环结束 p1将指向链表原来的最后一个节点，也就是新链表的头节点

代码

While (p2 !=null){
	*tmp=p2->next;
	p2->next=p1;
  p1=p2;p2=tmp;
}
return p1;

解答2 递归实现

假设链表为 1–>2–>3–>NULL

  • 思路就是从头到尾将每个元素开始依次入函数栈，同时如果是最后一个节点 则记录这个节点最后此节点作为新链表的头节点返回

    然后函数栈返回的时候，将当前节点的next节点的next指向当前节点 逐个完成反转 下面的网上找到的动图

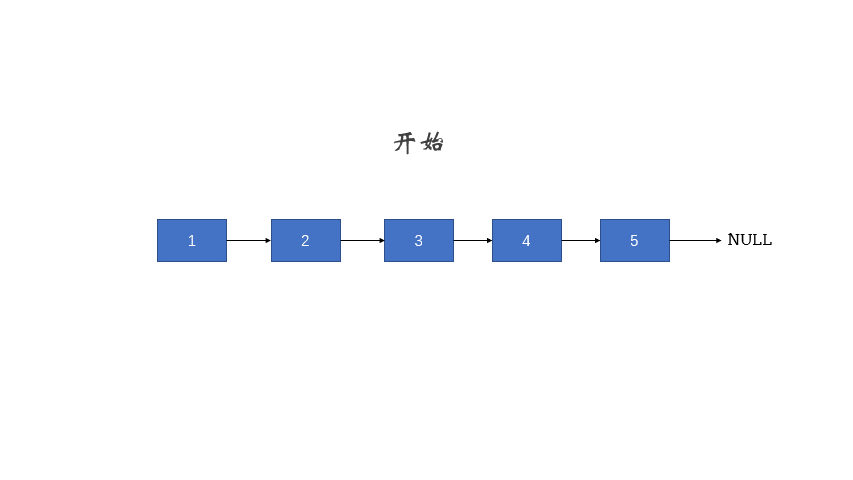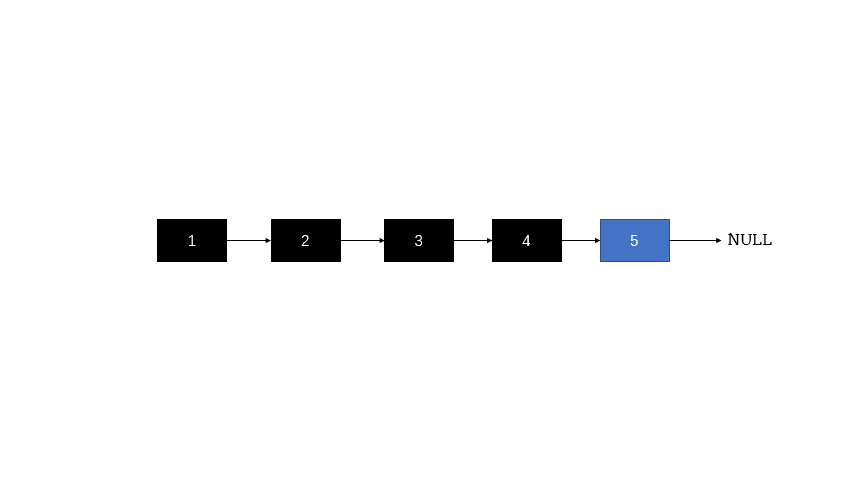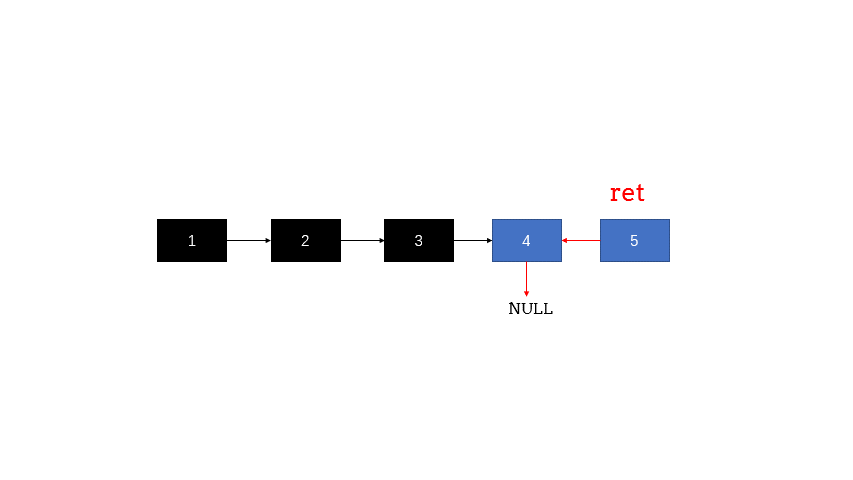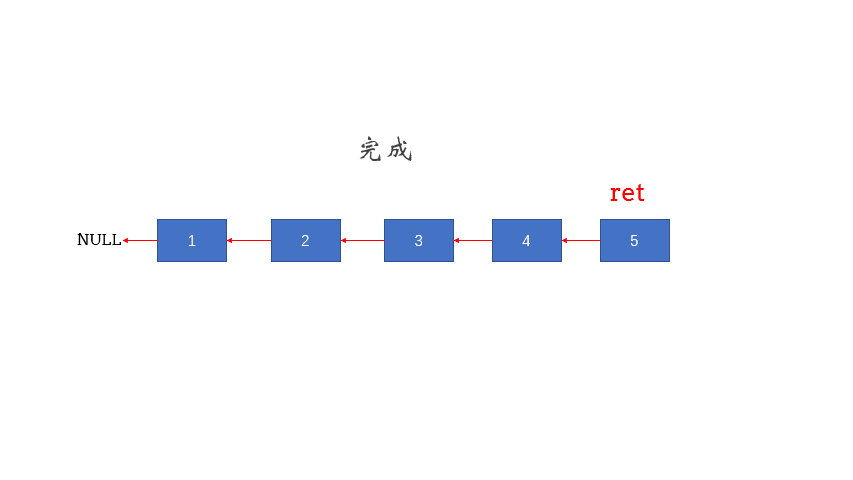
代码实现

Node* reverseList(Node* cur){
  if ( cur==NULL || cur->next==NULL){
    return cur;//如果当前节点为空 或者当前节点没有后继节点 那么直接返回当前节点即可
  }
  Node* ret=reverseList(cur->next);//将节点的next节点入函数栈 ret最后指向就是原链表最后一个节点
  cur->next->next=cur;//将当前节点的next节点的next节点 指向自己 完成局部反转
  cur->next=NULL;//将当前节点的next指针先指向NULL
}

求数组小和

题目描述

​ 在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组 的小和。例子: [1,3,4,2,5]

1左边比1小的数，没有;

3左边比3小的数，1;

4左边比4小的数，1、3;

2左边比2小的数，1;

5左边比5小的数，1、3、4、2;

所以小和为1+1+3+1+1+3+4+2=16

最简单的解法

int smallNum(int a[],int len){
    int num=0;
    for(int i=1;i<len;++i){
	    for(int j=0;j<i;++j){
		    if(a[j]<a[i]) num+=a[j];
        }
	}
    return num;
}

暴力搜索，针对每个元素 都遍历左边比它小的 然后累计，2层循环 时间复杂度O($N^2$)

归并排序优化到O(N*logN)

  • 左边比它小的数字相加 其实就是找一个数右边有多少个数比它大(假设为a) 那么这个数就会产生a*当前数的小和，所以归并排序的过程刚好可以加速，因为右边区间某个数如果比左边区间当前数大，那么右边区间这个数后面的所有元素都比左边区间这个数大

代码

归并排序求数组小和 ```c++ int merge2Slice(int a[],int l,int mid,int r){ int num=0; int *help= new int[r-l+1];//声明1个辅助数组 合并后先放入help数组 然后在copy回原数组 int l1=l,r1=mid,l2=mid+1,r2=r;//便于理解 分割成为2个区间 l1--r1 l2--r2 int cur1=l1,cur2=l2,hIndex=0;//刚开始下标分别指向2个区间的开始位置 辅助数组的下标刚开始赋值为0 while (cur1<=r1 && cur2<=r2 ){//任意1个区间遍历完成退出循环 if (a[cur1]>1 ); int smallNumL=mergeSortRecur(A,l,mid);//左半边归并排序 int smallNumR=mergeSortRecur(A,mid+1,r);//右半边归并排序 return smallNumL+smallNumR+merge2Slice(A,l,mid,r);//将2个分片合并 } ```

数组逆序对问题

题目描述

在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序对

暴力算法时间复杂度为O($N^2$)

也可以才有归并排序优化时间复杂度为O(NlogN)

代码 ```c++ //在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序 对 int getReversePairs(vector& nums){ int count=0; for (int i=0;inums[j]) count++; } } return count; } //采用归并排序优化 int merge2Slice1(vector& a,int l,int mid,int r){ int count=0; int *help= new int[r-l+1];//声明1个辅助数组 合并后先放入help数组 然后在copy回原数组 int l1=l,r1=mid,l2=mid+1,r2=r;//便于理解 分割成为2个区间 l1--r1 l2--r2 int cur1=l1,cur2=l2,hIndex=0;//刚开始下标分别指向2个区间的开始位置 辅助数组的下标刚开始赋值为0 while (cur1<=r1 && cur2<=r2 ){//任意1个区间遍历完成退出循环 if(a[cur2]& nums,int l,int r){ //base case 如果l==r 则直接返回 只有一个元素小和返回0 if (l==r){ return 0; } int mid=l + ( (r-l)>>1 ); int reParisNumL=mergeSortRecur1(nums,l,mid);//左半边归并排序 并返回逆序对数量 int reParisNumR=mergeSortRecur1(nums,mid+1,r);//右半边归并排序 return reParisNumL+reParisNumR+merge2Slice1(nums,l,mid,r);//将2个分片合并 } //在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序 归并排序优化版本 int getReversePairs1(vector& nums){ return mergeSortRecur1(nums,0,nums.size()-1); } ```

数组分区<=左边 >右边

//问题1
//给定一个数组arr，和一个数num，请把小于等于num的数放在数 组的左边，大于num的数放在数组的右边。
// 要求额外空间复杂度O(1)，时间复杂度O(N) 返回<=num的第后一个下标
int  partition1(int a[], int l, int r, int num) {
	int less = l - 1,cur=l;//指针先指向最左边元素的前一个位置 less为小于等于区域的边界 下标<=less的 都是<=num的
	while (cur<=r) {
		if (a[cur]<=num){//如果当前元素<=num 则将less下一个位置的元素 跟当前元素交换 同时less++ 扩大<=区域
            swap(a,++less,cur++);
        }else{
            cur++;
        }
	}
    return less;
}

荷兰国旗问题

//问题2 荷兰国旗
// 给定一个数组arr，和一个数num，请把小于num的数放在数组的 左边，等于num的数放在数组的中间，大于num的数放在数组的 右边。
// 要求额外空间复杂度O(1)，时间复杂度O(N)
void partition2(int arr[], int l, int r, int num,int& lastLess,int& firstMore) {
	int less = l - 1,cur=l;//less先指向最左边元素的前面一个位置   下标<=less的元素都为<num的区域
	int more = r + 1;//more先指向最右边边元素的后面一个位置 下标>=more的元素都为>num的区域
                     //同理 less+1-->more-1的区域为=num的区域
	while (cur < more) {//cur指针刚开始指向最左边的元素 如果碰到了more就说明遍历完成了
		if (arr[cur] < num) {//如果当前元素<num 则将less下一个位置的元素 跟当前元素交换 同时less++ 扩大<区域 cur++遍历下一个元素
			swap(arr, ++less, cur++);
		} else if (arr[cur] > num) {//如果当前元素>num 则将more下一个位置的元素 跟当前元素交换 同时more-- 扩大>区域 cur不能++因为 more前面的元素还没有遍历比较
			swap(arr, --more, cur);
		} else {
			cur++;//如果相等 cur直接++遍历下一个元素
		}
	}
    lastLess=less+1,firstMore=more-1;
    return;
}

荷兰国旗可以优化快速排序

数组中位数

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() - 返回目前所有元素的中位数。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

准备2个堆 一个大堆 一个小堆 一个个加入堆

  1. 如果大堆size为0 直接进大堆

  2. 如果<=大堆堆顶 进大堆

    加入后 判断大堆size-小堆size如果>=2 也就是大堆数据太多了 则弹出大堆的堆顶 放入小堆

  3. 如果>大堆堆顶 进小堆

    加入后 判断小堆size-大堆size如果>=2 也就是小堆数据太多了 则弹出小堆的堆顶 放入大堆

这样的操作下来 大堆小堆数据量平均 同时较小的部分都在大堆 较大的部分都在小堆 堆结构的堆顶又比较特殊，

所以大堆的堆顶 存放的是较小部分的最大值，小堆的堆顶存放的是较大部分的最小值 所以如果是偶数，直接2个堆顶相加除以2即可

如果是奇数，哪个堆size大就返回其堆顶

代码

求数组中位数 ```c++ class MedianFinder { public: /** initialize your data structure here. */ priority_queue maxq; priority_queue < int, vector, greater > minq; MedianFinder() { } void addNum(int num) { if (maxq.size()==0 ){//如果大顶堆为空 先插入大顶堆 maxq.push(num); }else if (num<=maxq.top()){//如果小于等于大顶堆的堆顶 则放入大顶堆 maxq.push(num); if ( maxq.size()-minq.size()>=2){//大顶堆放多了 将其堆顶弹出 放入小顶堆 minq.push(maxq.top()); maxq.pop(); } }else{//如果大于大顶堆的堆顶 则放入小顶堆 minq.push(num); if ( minq.size()-maxq.size()>=2){//小顶堆放多了 将其堆顶弹出 放入大顶堆 maxq.push(minq.top()); minq.pop(); } } } double findMedian() { if (minq.size()==0 && maxq.size()>0){ return double(maxq.top()); }else if( minq.size()>0 && maxq.size()>0){ if ( (minq.size()+maxq.size())%2==0){ return double(minq.top()+maxq.top())/2; }else{ return maxq.size()>minq.size()?maxq.top():minq.top(); } } return 0; } }; /** * Your MedianFinder object will be instantiated and called as such: * MedianFinder* obj = new MedianFinder(); * obj->addNum(num); * double param_2 = obj->findMedian(); */ ```

数组排序后相邻2位数的最大差值

题目描述

给定一个数组，求如果排序之后，相邻两数的最大差值，要求时 间复杂度O(N)，且要求不能用非基于比较的排序

思路

首先常见的基于比较的排序时间复杂度做不到O(N)，然后又不能用桶排序，所以其实就是想说能不能不排序，也能解决问题，这里用到桶排序的思想，但是不真正排序。

  1. 假设数组有N个数，先找到最小值min，最大值max，准备N+1个桶

  2. min放到0号桶 max放N+1号桶，其它数据按照一定规律分配到桶中 (int) ((num - min) * len / (max - min))，其中len为数组长度，num为某一个具体的数

    比如最小值0 最大值99，数组长度60 每个桶可以承载的数量是平均的，因为有N+1个桶，所以一定有桶是空的，因为每个桶容量平均，所以最大差值一定不在桶内产生，所以每个桶只需要记录入桶的最大最小值以及是否有数据入桶即可，比较所有相邻的非空桶，后面桶的最小减去前面桶的最大就是差值，遍历找到最大差值即可

代码

不排序求数组中相邻2个数的最大差值O(N) ```c++ // 给定一个数组，求如果排序之后，相邻两数的最大差值，要求时 间复杂度O(N)，且要求不能用非基于比较的排序。 #include #include #include using namespace std; struct Node{ Node():isIn(false),min(INT_MAX),max(INT_MIN){} bool isIn;//是否入桶了 int min; int max; }; //传入数组元素num 数组长度len 数组中最小值min，最大值max 返回元素num应该放到第几号桶 int bucket(long num, long len, long min, long max) { return (int) ((num - min) * len / (max - min));//min在0桶 max在最后一个桶 } int maxGap(int nums[],int len) { if (len < 2) { return 0; } int min = INT_MAX; int max = INT_MIN; for (int i = 0; i < len; i++) {//遍历找到最大最小值 min = std::min(min, nums[i]); max = std::max(max, nums[i]); } if (min == max) {//如果最大最小值相等 则直接返回0 即可 return 0; } vector help(len+1);//辅助数组 int bid = 0;//计算得到放到第几号桶 for (int i = 0; i < len; i++) { bid = bucket(nums[i], len, min, max); if (!help[i].isIn){ help[i].min=help[i].max=nums[i]; help[i].isIn=true; }else{ help[i].min=std::min(help[i].min,nums[i]); help[i].max=std::max(help[i].max,nums[i]); } } int res = 0; int lastMax = help[0].max;//保存前一个非空桶中的最大值 刚开始为0号桶的最大值 int i = 1; for (; i <= len; i++) {//从1号桶开始遍历 0号桶一定不空因为放了min if (help[i].isIn) { res = std::max(res, help[i].min - lastMax);// 相邻2个非空桶 后一个的min-前一个max就是可能的最大差值 res保存最大差值 lastMax = help[i].max; } } return res; } ```

数组实现大小固定的队列和栈

栈

  • 实现栈比较简单，定义一个指针或者说int类型的下标，刚开始指向0号下标位置，insertIndex刚开始赋值为0，顾名思义，insertIndex就是新插入元素的位置
    • 每次插入元素insertIndex++
    • 每次弹出元素，对应下标为 insertIndex-1,弹出后insertIndex–
    • 边界值控制 insertIndex为0 不能弹出，insertIndex为数组长度，也就是最后一个元素后面，不能再插入。

栈代码

数组实现固定大小的栈 ```c++ template struct ArrayStack { private: T* data;//数组指针 int insIndex;//保存下一个push元素时对应的插入位置指针 也可以由其计算出当前栈真正的元素个数 int capacity;//最大容量 public: ArrayStack(int intiCapacity) { data=new T[intiCapacity]; capacity=intiCapacity; insIndex=0;//插入位置刚赋值为0 } T peek() ;//返回栈顶元素值 不弹出 void push(T t);//压栈操作 T pop();//出栈操作 int getSize(){//返回当前栈有多少个元素 return insIndex; } ~ArrayStack(){ delete[] data; } }; template void ArrayStack::push(T t){ if(insIndex==capacity){//可插入下标==最大容量 说栈已经满了 throw std::runtime_error("stack is full,no left space to push"); } data[insIndex++]=t;//在insIndex位置插入元素，同时insIndex++ } template T ArrayStack::peek(){ if( insIndex>0){//如果栈内有数据 返回栈顶元素 也就是insIndex-1的位置的元素 return data[insIndex-1]; }else{ throw std::runtime_error("stack is empty"); } } template T ArrayStack::pop(){ if( insIndex>0){//如果栈内有数据 弹出栈顶元素 也就是insIndex-1的位置的元素 同时insIndex-- return data[--insIndex]; }else{ throw std::runtime_error("stack is empty"); } } ```

队列

  • 实现队列比实现栈多了一些内容，但也比较好理解 刻印设计2个指针 一个size变量

    head指向队列头，insertIndex指向下一个可以插入的位置，2个指针的循环顺序都是0—>size-1—>0循环使用 刚开始都指向0下标

    • 插入元素insertIndex++ ，head不动 size++ (size如果为最大容量 不给插入 报错)
    • 弹出元素 head++，insertIndex不变(size如果为0 不给弹出 报错)

代码实现

数组实现的固定长度的队列 ```c++ //数组实现的固定大小长度的队列 template struct ArrayQueue { private: T* data;//数组指针 int head;//队列头的下标 int insIndex;//保存下一个push元素时对应的插入位置指针 也可以由其计算出当前队列真正的元素个数 int capacity;//最大容量 int size;//当前队列的真实数据个数 public: ArrayQueue(int intiCapacity) { data=new T[intiCapacity]; capacity=intiCapacity; head=insIndex=size=0;//插入位置赋值为0 头指针为0 队列size为0 } T top() ;//返回队列头 元素值 不弹出 void push(T t);//入队操作 T pop();//出队操作 int getSize(){//返回当前队列有多少个元素 return size; } ~ArrayQueue(){ delete[] data; } }; template void ArrayQueue::push(T t){ if(size==capacity){//当前队列已经到达最大容量 说队列已经满了 throw std::runtime_error("queue is full,no left space to push"); } data[insIndex++]=t;//在insIndex位置插入元素，同时insIndex++ if ( insIndex==capacity){//循环从0开始 insIndex=0; } size++; //push操作 head不变 } template T ArrayQueue::top(){ if( size>0){//如果队列内有数据 返回队列头元素 也就是head位置的元素 return data[head]; }else{ throw std::runtime_error("queue is empty"); } } template T ArrayQueue::pop(){ if( size>0){//如果队列内有数据 弹出队列头元素 也就是head位置的元素 size--; //insIndex不变 int oldHead=head; head++; if ( head==capacity){//循环从0开始 head=0; } return data[oldHead]; }else{ throw std::runtime_error("queue is empty"); } } ```

队列实现栈

  • 准备2个队列，一个insQ 一个helpQ 刚开始都为空
  • 插入都是插入到insQ helpQ不动
  • 弹出操作逻辑如下:
    1. 将insQ依次出对(insQ队尾不出) 依次入对到helpQ
    2. 此时insQ只剩下队尾 然后弹出 返回(如果是peek操作 insQ队尾弹出后 需要也入对到helpQ)
    3. 将insQ和helpQ的指向互换即可

栈实现队列

  • 准备2个栈 一个是push栈一个是pop栈
  • 插入都是插入push栈
  • 弹出操作如下：
    1. 如果pop栈为空 将push栈元素全部出栈 然后依次入栈道pop栈，最后弹出pop栈的栈顶(当时push栈最先插入的元素)
    2. 如果pop栈不为空 直接将pop栈的栈顶弹出

动物收容所

题目描述

动物收容所。有家动物收容所只收容狗与猫，且严格遵守“先进先出”的原则。在收养该收容所的动物时，收养人只能收养所有动物中“最老”（由其进入收容所的时间长短而定）的动物，或者可以挑选猫或狗（同时必须收养此类动物中“最老”的）。换言之，收养人不能自由挑选想收养的对象。请创建适用于这个系统的数据结构，实现各种操作方法，比如enqueue、dequeueAny、dequeueDog和dequeueCat。允许使用Java内置的LinkedList数据结构。enqueue方法有一个animal参数，animal[0]代表动物编号，animal[1]代表动物种类，其中 0 代表猫，1 代表狗。dequeue*方法返回一个列表[动物编号, 动物种类]，若没有可以收养的动物，则返回[-1,-1]。

示例1: 输入： [“AnimalShelf”, “enqueue”, “enqueue”, “dequeueCat”, “dequeueDog”, “dequeueAny”] [[], [[0, 0]], [[1, 0]], [], [], []] 输出： [null,null,null,[0,0],[-1,-1],[1,0]] 示例2: 输入： [“AnimalShelf”, “enqueue”, “enqueue”, “enqueue”, “dequeueDog”, “dequeueCat”, “dequeueAny”] [[], [[0, 0]], [[1, 0]], [[2, 1]], [], [], []] 输出： [null,null,null,null,[2,1],[0,0],[1,0]]来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/animal-shelter-lcci 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

  1. 肯定是2个队列 一个猫 一个狗。指定要狗或者猫，非常简单，直接从相应队列出队1个即可
  2. 如果不指定猫狗，就需要比较猫队头和狗队头谁进来的早(可以设计一个计数器，进来早的小，进来晚的大，返回计数器小的就行)，力扣上直接给动物编号了 直接用就行

代码

猫狗收容所c++ ```c++ class AnimalShelf { public: AnimalShelf() { } void enqueue(vector animal) { if (animal.at(1) == 0) //动物种类：猫 { m_queue_cat.push(animal); } else { m_queue_dog.push(animal); } } vector dequeueAny() { vector animal; if (m_queue_cat.empty() && m_queue_dog.empty()) { return vector{-1, -1}; } else if (!m_queue_cat.empty() && m_queue_dog.empty()) { animal = m_queue_cat.front(); m_queue_cat.pop(); } else if (m_queue_cat.empty() && !m_queue_dog.empty()) { animal = m_queue_dog.front(); m_queue_dog.pop(); } else { //用2个队列分别保存猫狗，而且要有个数据保存进来的编号，或者说是第几个进来的，这里动物编号就是这个意思了 所以直接使用就行 猫狗都有的时候 要看猫狗队头的编号 谁小给谁 if (m_queue_cat.front().at(0) < m_queue_dog.front().at(0)) //动物编号：猫 < 狗 猫先出 { animal = m_queue_cat.front(); m_queue_cat.pop(); } else { animal = m_queue_dog.front(); m_queue_dog.pop(); } } return animal; } vector dequeueDog() { if (m_queue_dog.empty()) { return vector{-1, -1}; } vector dog = m_queue_dog.front(); m_queue_dog.pop(); return dog; } vector dequeueCat() { if (m_queue_cat.empty()) { return vector{-1, -1}; } vector cat = m_queue_cat.front(); m_queue_cat.pop(); return cat; } private: queue> m_queue_cat; queue> m_queue_dog; }; // 作者：eric-345 // 链接：https://leetcode-cn.com/problems/animal-shelter-lcci/solution/c-mao-gou-liang-ge-dui-lie-by-eric-345/ // 来源：力扣（LeetCode） // 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 /** * Your AnimalShelf object will be instantiated and called as such: * AnimalShelf* obj = new AnimalShelf(); * obj->enqueue(animal); * vector param_2 = obj->dequeueAny(); * vector param_3 = obj->dequeueDog(); * vector param_4 = obj->dequeueCat(); */ ```

顺时针转圈打印矩阵

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5] 示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：

  • 实现一个函数 画一个矩形，左上方一个点到右下方一个点
  • 然后循环画矩形 比如下图 下画(0,0)–>(3,3) 顺时针打印矩阵2

  • 然后xy坐标都+1 画(1,1)–(2,2)

代码

顺时针转圈打印矩阵 代码非本人 ```c++ //给出左上方坐标 右下方坐标 顺时针画圈 void printSquare(int leftUp[], int rigthDown[],int matrix[][FACTORIAL]){ int i = leftUp[0], j = leftUp[1]; while (j < rigthDown[1]) { printf("%d ", matrix[i][j++]); } while (i < rigthDown[0]) { printf("%d ", matrix[i++][j]); } while (j > leftUp[1]) { printf("%d ", matrix[i][j--]); } while (i > leftUp[0]) { printf("%d ", matrix[i--][j]); } } //循环打印圈圈 也就是从外到内 void printMatrixCircled(int matrix[][FACTORIAL]){ int leftUp[] = {0, 0}, rightDown[] = {FACTORIAL-1,FACTORIAL-1}; while (leftUp[0] < rightDown[0] && leftUp[1] < rightDown[1]) { printSquare(leftUp, rightDown, matrix); ++leftUp[0]; ++leftUp[1]; --rightDown[0]; --rightDown[1]; } } int main(){ int matrix[4][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16} }; printMatrixCircled(matrix);//1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10 } ```

旋转方块矩阵(正方形)

题目描述

旋转正方形矩阵 【题目】 给定一个整型正方形矩阵matrix，请把该矩阵调整成 顺时针旋转90度的样子。 【要求】 额外空间复杂度为O(1)。

思路

  1. 设计一个函数 每次只旋转4个坐标点
  2. 刚开始为正方形的四个顶边坐标 然后依次顺时针推进再找4个点 外圈没了搞内圈

代码

旋转方块矩阵 代码非本人 ```c++ //每次选取4个坐标 旋转 void circleSquare(int leftUp[],int rightDown[],int matrix[][FACTORIAL]){ int p1[] = {leftUp[0], leftUp[1]}; int p2[] = {leftUp[0], rightDown[1]}; int p3[] = {rightDown[0], rightDown[1]}; int p4[] = {rightDown[0],leftUp[1]}; while (p1[1] < rightDown[1]) { //swap int tmp = matrix[p4[0]][p4[1]]; matrix[p4[0]][p4[1]] = matrix[p3[0]][p3[1]]; matrix[p3[0]][p3[1]] = matrix[p2[0]][p2[1]]; matrix[p2[0]][p2[1]] = matrix[p1[0]][p1[1]]; matrix[p1[0]][p1[1]] = tmp; 
    p1[1]++;
    p2[0]++;
    p3[1]--;
    p4[0]--;
}

} //循环调用4坐标旋转函数，将所有坐标旋转完毕
void circleMatrix(int matrix[][FACTORIAL]){ int leftUp[] = {0, 0}, rightDown[] = {FACTORIAL - 1, FACTORIAL - 1}; while (leftUp[0] < rightDown[0] && leftUp[1] < rightDown[1]) { circleSquare(leftUp, rightDown, matrix); leftUp[0]++; leftUp[1]++; –rightDown[0]; –rightDown[1]; } } void printMatrix(int matrix[][FACTORIAL]){ for (int i = 0; i < FACTORIAL; ++i) { for (int j = 0; j < FACTORIAL; ++j) { printf("%2d “, matrix[i][j]); } printf("\n”); } } int main(){ int matrix[FACTORIAL][FACTORIAL] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16} }; printMatrix(matrix); circleMatrix(matrix); printMatrix(matrix); }

</details>

特殊的栈(O(1)返回最小值)

实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返 回栈中最小元素的操作

思路：

再准备一个辅助栈(保存的是当前栈的最小值)，

  1. 正常压栈的时候，如果辅助栈为空，也就是压入第一个元素，也将首元素压入辅助栈
  2. 再次压栈的时候跟辅助栈栈顶比较取最小值 压入辅助栈，栈顶还是最小也压入
  3. 出栈的时候 2个栈同时出栈

之字形打印矩阵

题目描述

之”字形打印矩阵 【题目】 给定一个矩阵matrix，按照“之”字形的方式打印这 个矩阵，例如:1 2 3 45 6 7 89 10 11 12 “之”字形打印的结果为:1，2，5，9，6，3，4，7，10，11， 8，12 【要求】 额外空间复杂度为O(1)。

思路

  1. 设计一个函数，能够在2个坐标之间画斜线 比如(0,2)—>(2.0) 就要经过3、8、13三个点
  2. 然后搞2个指针 刚开始都指向(0,0),然后一个只能往下走(走到底就只能往右)，一个只能往右走(走到底就只能往下)，每次都同时走一步，然后画出这2个点之间的线，同时注意方向即可

代码

之字形打印矩阵 代码分本人 ```c++ // const int rows = 3; const int cols = 6; //在2点之间画线，方向会依次相反 void printLine(int leftDown[],int rightUp[], bool turnUp,int matrix[rows][cols]){ int i,j; if (turnUp) { i = leftDown[0], j = leftDown[1]; while (j <= rightUp[1]) { printf("%d ", matrix[i--][j++]); } } else { i = rightUp[0], j = rightUp[1]; while (i <= leftDown[0]) { printf("%d ", matrix[i++][j--]); } } } //整2个指针 刚开始都指向(0,0) 刚开始都指向(0,0),然后一个只能往下走(走到底就只能往右)，一个只能往右走(走到底就只能往下)，每次都同时走一步，然后画出这2个点之间的线 void zigZagPrintMatrix(int matrix[rows][cols]){ if (matrix==NULL) return; int leftDown[] = {0, 0}, rightUp[] = {0, 0}; bool turnUp = true; while (leftDown[1] <= cols - 1) { printLine(leftDown, rightUp, turnUp, matrix); turnUp = !turnUp; if (leftDown[0] < rows - 1) { leftDown[0]++; } else { leftDown[1]++; } if (rightUp[1] < cols - 1) { ++rightUp[1]; } else { ++rightUp[0]; } } } int main(){ int matrix[rows][cols] = { {1, 2, 3, 4, 5, 6}, {7, 8, 9, 10, 11, 12}, {13, 14, 15, 16, 17, 18} }; zigZagPrintMatrix(matrix);//1 2 7 13 8 3 4 9 14 15 10 5 6 11 16 17 12 18 return 0; } ```

在行列都排好序的矩阵中找数

题目描述

在行列都排好序的矩阵中找数 【题目】 给定一个有N*M的整型矩阵matrix和一个整数K， matrix的每一行和每一 列都是排好序的。实现一个函数，判断K 是否在matrix中。 例如: 0 1 2 5 2 3 4 7 4 4 4 8 5 7 7 9 如果K为7，返回true;如果K为6，返 回false。 【要求】 时间复杂度为O(N+M)，额外空间复杂度为O(1)。

思路

因为行列都已经排好序了，所以就不需要完全遍历了

可以几个极点出发，慢慢扩散 下面假设从右上角的极点出发

  1. 大于该极点的值 就往下走 4—>8 (不能往左走，因为4左边的数都比它小)
  2. 如果小于该极点的值,(假设来到了8，我们要找6)，就往左走(因为8列下面的都比8大)
  3. 列不能超出最大列 行不能超过最大行

所以找6的过程如下：

  1. 6>4 往下走
  2. 6<8 往左走
  3. 6>5 往下走
  4. 6<7 往左走
  5. 6==6 找到

代码

在行列都排好序的数组中找数 代码分本人 ```c++ #include const int rows = 4; const int cols = 4; //大于该极点的值 就往下走 //如果小于该极点的值 就往左走 bool findNumInSortedMatrix(int num,int matrix[rows][cols]){ int i = 0, j = cols - 1; while (i <= rows - 1 && j <= cols - 1) { if (matrix[i][j] > num) { --j; } else if (matrix[i][j] < num) { ++i; } else { return true; } } return false; } int main(){ int matrix[rows][cols] = { {1, 2, 3, 4}, {2, 4, 5, 8}, {3, 6, 7, 9}, {4, 8, 9, 10} }; if (findNumInSortedMatrix(7, matrix)) { printf("find!"); } else { printf("not exist!"); } return 0; } ```

判断链表是否为回文结构(正反一样)

思路

用栈

  1. 遍历链表 依次压栈
  2. 再次遍历链表 依次入栈 逐一比较是否相等，不能就是false，都相等就是true

反转后半段链表

​ 快慢指针，反转后半段链表，然后左右往中间夹逼，判断逐一相等

代码

是否回文链表 ```java // need n extra space public static boolean isPalindrome1(Node head) { Stack stack = new Stack(); Node cur = head; while (cur != null) { stack.push(cur); cur = cur.next; } while (head != null) { if (head.value != stack.pop().value) { return false; } head = head.next; } return true; } // need n/2 extra space public static boolean isPalindrome2(Node head) { if (head == null || head.next == null) { return true; } Node right = head.next; Node cur = head; while (cur.next != null && cur.next.next != null) { right = right.next; cur = cur.next.next; } Stack stack = new Stack(); while (right != null) { stack.push(right); right = right.next; } while (!stack.isEmpty()) { if (head.value != stack.pop().value) { return false; } head = head.next; } return true; } // need O(1) extra space public static boolean isPalindrome3(Node head) { if (head == null || head.next == null) { return true; } Node n1 = head; Node n2 = head; while (n2.next != null && n2.next.next != null) { // find mid node n1 = n1.next; // n1 -> mid n2 = n2.next.next; // n2 -> end } n2 = n1.next; // n2 -> right part first node n1.next = null; // mid.next -> null Node n3 = null; while (n2 != null) { // right part convert n3 = n2.next; // n3 -> save next node n2.next = n1; // next of right node convert n1 = n2; // n1 move n2 = n3; // n2 move } n3 = n1; // n3 -> save last node n2 = head;// n2 -> left first node boolean res = true; while (n1 != null && n2 != null) { // check palindrome if (n1.value != n2.value) { res = false; break; } n1 = n1.next; // left to mid n2 = n2.next; // right to mid } n1 = n3.next; n3.next = null; while (n1 != null) { // recover list n2 = n1.next; n1.next = n3; n3 = n1; n1 = n2; } return res; } ```

链表按某元素值分区间(< = >)

题目描述

将单向链表按某值划分成左边小、中间相等、右边大的形式 【题目】 给定一个单向链表的头节点head，节点的值类型是整型，再给定一个 整 数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于 pivot 的节点，中间部分都是值等于pivot的节点，右部分都是值大于 pivot的节点。 除这个要求外，对调整后的节点顺序没有更多的要求。 例如:链表9->0->4->5- >1，pivot=3。 调整后链表可以是1->0->4->9->5，也可以是0->1->9->5->4。总 之，满 足左部分都是小于3的节点，中间部分都是等于3的节点(本例中这个部 分为空)，右部分都是大于3的节点即可。对某部分内部的节点顺序不做 要求。

进阶: 在原问题的要求之上再增加如下两个要求。 在左、中、右三个部分的内部也做顺序要求，要求每部分里的节点从左 到右的 顺序与原链表中节点的先后次序一致。 例如:链表9->0->4->5->1，pivot=3。 调整后的链表是0->1->9->4->5。 在满足原问题要求的同时，左部分节点从左到 右为0、1。在原链表中也 是先出现0，后出现1;中间部分在本例中为空，不再 讨论;右部分节点 从左到右为9、4、5。在原链表中也是先出现9，然后出现4， 最后出现5。 如果链表长度为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

思路

  1. 链表cp到数组 荷兰国旗问题搞定 不稳定 需要O(N)辅助空间
  2. 遍历2遍数组 2.1. 第一遍遍历 得到第一个小于元素值的节点 第一个等于元素值的节点 第一个大于元素值的节点 2.2. 第二遍遍历 <num不是第一个小于的节点 挂到FirstLess后面 稳定 等于大于情况一样 把一个链表拆成了3个链表 2.3. 拼接3个链表

代码

javacode ```java package class_03; public class Code_12_SmallerEqualBigger { public static class Node { public int value; public Node next; public Node(int data) { this.value = data; } } public static Node listPartition1(Node head, int pivot) { if (head == null) { return head; } Node cur = head; int i = 0; while (cur != null) { i++; cur = cur.next; } Node[] nodeArr = new Node[i]; i = 0; cur = head; for (i = 0; i != nodeArr.length; i++) { nodeArr[i] = cur; cur = cur.next; } arrPartition(nodeArr, pivot); for (i = 1; i != nodeArr.length; i++) { nodeArr[i - 1].next = nodeArr[i]; } nodeArr[i - 1].next = null; return nodeArr[0]; } public static void arrPartition(Node[] nodeArr, int pivot) { int small = -1; int big = nodeArr.length; int index = 0; while (index != big) { if (nodeArr[index].value < pivot) { swap(nodeArr, ++small, index++); } else if (nodeArr[index].value == pivot) { index++; } else { swap(nodeArr, --big, index); } } } public static void swap(Node[] nodeArr, int a, int b) { Node tmp = nodeArr[a]; nodeArr[a] = nodeArr[b]; nodeArr[b] = tmp; } public static Node listPartition2(Node head, int pivot) { Node sH = null; // small head Node sT = null; // small tail Node eH = null; // equal head Node eT = null; // equal tail Node bH = null; // big head Node bT = null; // big tail Node next = null; // save next node // every node distributed to three lists while (head != null) { next = head.next; head.next = null; if (head.value < pivot) { if (sH == null) { sH = head; sT = head; } else { sT.next = head; sT = head; } } else if (head.value == pivot) { if (eH == null) { eH = head; eT = head; } else { eT.next = head; eT = head; } } else { if (bH == null) { bH = head; bT = head; } else { bT.next = head; bT = head; } } head = next; } // small and equal reconnect if (sT != null) { sT.next = eH; eT = eT == null ? sT : eT; } // all reconnect if (eT != null) { eT.next = bH; } return sH != null ? sH : eH != null ? eH : bH; } public static void printLinkedList(Node node) { System.out.print("Linked List: "); while (node != null) { System.out.print(node.value + " "); node = node.next; } System.out.println(); } public static void main(String[] args) { Node head1 = new Node(7); head1.next = new Node(9); head1.next.next = new Node(1); head1.next.next.next = new Node(8); head1.next.next.next.next = new Node(5); head1.next.next.next.next.next = new Node(2); head1.next.next.next.next.next.next = new Node(5); printLinkedList(head1); // head1 = listPartition1(head1, 4); head1 = listPartition2(head1, 5); printLinkedList(head1); } } ```

打印链表公共部分

打印两个有序链表的公共部分 【题目】 给定两个有序链表的头指针head1和head2，打印两个 链表的公共部分。

思路

链表有序，从头遍历，谁小谁往后移动，相等就打印

复制含有随机指针节点的链表

题目描述

【题目】 一种特殊的链表节点类描述如下: public class Node { public int value; public Node next; public Node rand; public Node(int data) { this.value = data; } } Node类中的value是节点值，next指针和正常单链表中next指针的意义 一 样，都指向下一个节点，rand指针是Node类中新增的指针，这个指 针可 能指向链表中的任意一个节点，也可能指向null。 给定一个由 Node节点类型组成的无环单链表的头节点head，请实现一个 函数完成 这个链表中所有结构的复制，并返回复制的新链表的头节点。 进阶: 不使用额外的数据结构，只用有限几个变量，且在时间复杂度为 O(N) 内完成原问题要实现的函数。

思路

  • 遍历复制节点本身没有问题 但是不能复制随机指针节点
  • 第一种方案就是使用hashmap，第一次遍历复制节点，同时加入map[oldNode]=newNode;这个map就保存了新旧节点的对应关系 第二次遍历，找到oldNode的随机节点oldRandom，通过map找到对应的新节点newNode,和newRandDom,设置即可。这种空间复杂度为O(N)
  • 第二种方案不用hashmap但是借鉴其思想，主要就是保存新旧节点的对应关系，第一次遍历搞成下面的链表结构: oldNode1—>newNode1—>oldNode2—->newNode2—,这样以来新旧node的对应关系就保存下来了，旧节点的next就是其新节点

​ 第二次遍历就 newNode1.RandomNode=oldNode1.Random即可 同时next指向newNode2

代码

复制含有随机指针节点的链表 java ```Java package class_03; import java.util.HashMap; public class Code_13_CopyListWithRandom { public static class Node { public int value; public Node next; public Node rand; public Node(int data) { this.value = data; } } public static Node copyListWithRand1(Node head) { HashMap map = new HashMap(); Node cur = head; while (cur != null) { map.put(cur, new Node(cur.value)); cur = cur.next; } cur = head; while (cur != null) { map.get(cur).next = map.get(cur.next); map.get(cur).rand = map.get(cur.rand); cur = cur.next; } return map.get(head); } public static Node copyListWithRand2(Node head) { if (head == null) { return null; } Node cur = head; Node next = null; // copy node and link to every node while (cur != null) { next = cur.next; cur.next = new Node(cur.value); cur.next.next = next; cur = next; } cur = head; Node curCopy = null; // set copy node rand while (cur != null) { next = cur.next.next; curCopy = cur.next; curCopy.rand = cur.rand != null ? cur.rand.next : null; cur = next; } Node res = head.next; cur = head; // split while (cur != null) { next = cur.next.next; curCopy = cur.next; cur.next = next; curCopy.next = next != null ? next.next : null; cur = next; } return res; } public static void printRandLinkedList(Node head) { Node cur = head; System.out.print("order: "); while (cur != null) { System.out.print(cur.value + " "); cur = cur.next; } System.out.println(); cur = head; System.out.print("rand: "); while (cur != null) { System.out.print(cur.rand == null ? "- " : cur.rand.value + " "); cur = cur.next; } System.out.println(); } public static void main(String[] args) { Node head = null; Node res1 = null; Node res2 = null; printRandLinkedList(head); res1 = copyListWithRand1(head); printRandLinkedList(res1); res2 = copyListWithRand2(head); printRandLinkedList(res2); printRandLinkedList(head); System.out.println("========================="); head = new Node(1); head.next = new Node(2); head.next.next = new Node(3); head.next.next.next = new Node(4); head.next.next.next.next = new Node(5); head.next.next.next.next.next = new Node(6); head.rand = head.next.next.next.next.next; // 1 -> 6 head.next.rand = head.next.next.next.next.next; // 2 -> 6 head.next.next.rand = head.next.next.next.next; // 3 -> 5 head.next.next.next.rand = head.next.next; // 4 -> 3 head.next.next.next.next.rand = null; // 5 -> null head.next.next.next.next.next.rand = head.next.next.next; // 6 -> 4 printRandLinkedList(head); res1 = copyListWithRand1(head); printRandLinkedList(res1); res2 = copyListWithRand2(head); printRandLinkedList(res2); printRandLinkedList(head); System.out.println("========================="); } } ```

两个链表是否相交

这个问题要区分链表是否有环，所以先看是否有环。

判断链表是否有环

  • 第一种 准备一个hash表，然后遍历链表，如果节点不在hash中，则加入，如果在hash中则说明存在环，而且第一个在hash中的节点就是第一个入环的节点
  • 第二种 准备2个指针，快(f)慢(s)指针(刚开始都指向第一个节点)，然后快指针一次走2步,慢指针一次走1步，如果快慢指针撞上了就是有环，这个时候将快指针指向第一个节点，然后快慢指针每次都走一步，再次撞上的节点就是第一个入环的节点(数学可以证明这个方法是正确的，不用纠结)

两个无环链表可能相交，最后一个节点必定为同一个节点

这种可以有hash，也可以不用hash。
  1. 用hash，就将链表1 依次入到hash，然后遍历链表2 第一个在hash中存在的节点就是2个链表相交的节点
  2. 不用hash，遍历2个链表，分别得到len1,endNode1,len2,endnode2,如果endNode1==endNode2，则2个链表相交，找到最长的链表，先走(abs(len1-len2))步，然后2个链表都依次走1步 第一个撞上的节点就是相交的节点

两个无环链表和一个有环链表不可能相交 因为是单链表

两个有环链表可能相交

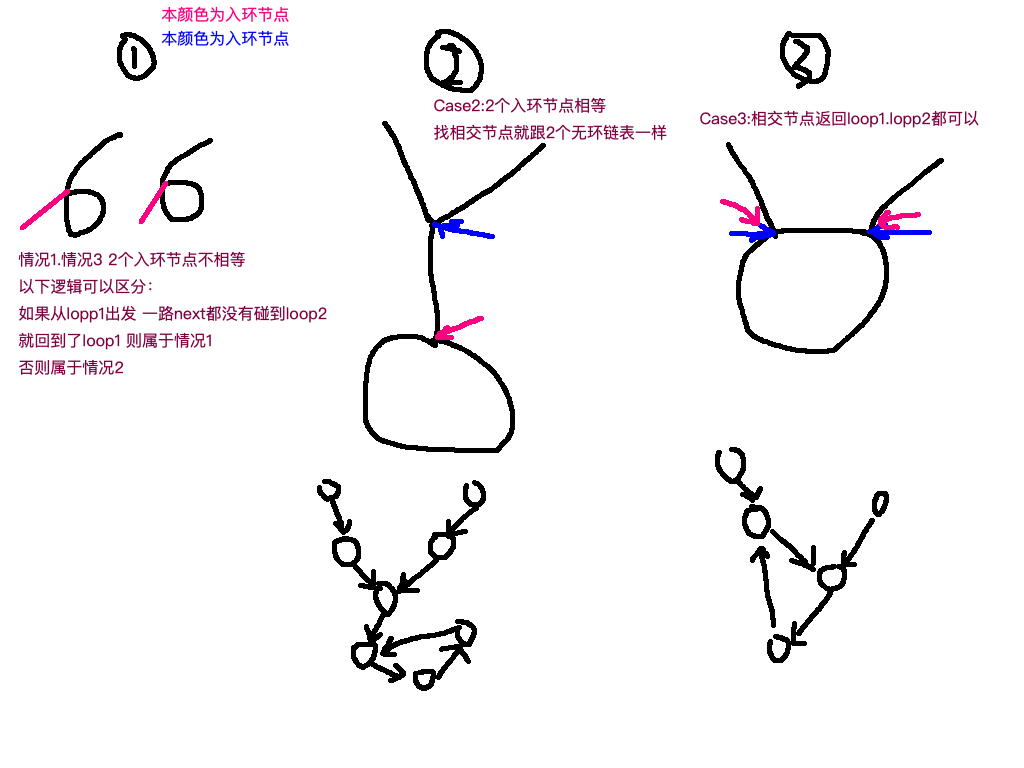
代码

链表相交问题 ```Java package class_03; public class Code_14_FindFirstIntersectNode { public static class Node { public int value; public Node next; public Node(int data) { this.value = data; } } public static Node getIntersectNode(Node head1, Node head2) { if (head1 == null || head2 == null) { return null; } Node loop1 = getLoopNode(head1); Node loop2 = getLoopNode(head2); if (loop1 == null && loop2 == null) { return noLoop(head1, head2); } if (loop1 != null && loop2 != null) { return bothLoop(head1, loop1, head2, loop2); } return null; } public static Node getLoopNode(Node head) { if (head == null || head.next == null || head.next.next == null) { return null; } Node n1 = head.next; // n1 -> slow Node n2 = head.next.next; // n2 -> fast while (n1 != n2) { if (n2.next == null || n2.next.next == null) { return null; } n2 = n2.next.next; n1 = n1.next; } n2 = head; // n2 -> walk again from head while (n1 != n2) { n1 = n1.next; n2 = n2.next; } return n1; } public static Node noLoop(Node head1, Node head2) { if (head1 == null || head2 == null) { return null; } Node cur1 = head1; Node cur2 = head2; int n = 0; while (cur1.next != null) { n++; cur1 = cur1.next; } while (cur2.next != null) { n--; cur2 = cur2.next; } if (cur1 != cur2) { return null; } cur1 = n > 0 ? head1 : head2; cur2 = cur1 == head1 ? head2 : head1; n = Math.abs(n); while (n != 0) { n--; cur1 = cur1.next; } while (cur1 != cur2) { cur1 = cur1.next; cur2 = cur2.next; } return cur1; } public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) { Node cur1 = null; Node cur2 = null; if (loop1 == loop2) { cur1 = head1; cur2 = head2; int n = 0; while (cur1 != loop1) { n++; cur1 = cur1.next; } while (cur2 != loop2) { n--; cur2 = cur2.next; } cur1 = n > 0 ? head1 : head2; cur2 = cur1 == head1 ? head2 : head1; n = Math.abs(n); while (n != 0) { n--; cur1 = cur1.next; } while (cur1 != cur2) { cur1 = cur1.next; cur2 = cur2.next; } return cur1; } else { cur1 = loop1.next; while (cur1 != loop1) { if (cur1 == loop2) { return loop1; } cur1 = cur1.next; } return null; } } public static void main(String[] args) { // 1->2->3->4->5->6->7->null Node head1 = new Node(1); head1.next = new Node(2); head1.next.next = new Node(3); head1.next.next.next = new Node(4); head1.next.next.next.next = new Node(5); head1.next.next.next.next.next = new Node(6); head1.next.next.next.next.next.next = new Node(7); // 0->9->8->6->7->null Node head2 = new Node(0); head2.next = new Node(9); head2.next.next = new Node(8); head2.next.next.next = head1.next.next.next.next.next; // 8->6 System.out.println(getIntersectNode(head1, head2).value); // 1->2->3->4->5->6->7->4... head1 = new Node(1); head1.next = new Node(2); head1.next.next = new Node(3); head1.next.next.next = new Node(4); head1.next.next.next.next = new Node(5); head1.next.next.next.next.next = new Node(6); head1.next.next.next.next.next.next = new Node(7); head1.next.next.next.next.next.next = head1.next.next.next; // 7->4 // 0->9->8->2... head2 = new Node(0); head2.next = new Node(9); head2.next.next = new Node(8); head2.next.next.next = head1.next; // 8->2 System.out.println(getIntersectNode(head1, head2).value); // 0->9->8->6->4->5->6.. head2 = new Node(0); head2.next = new Node(9); head2.next.next = new Node(8); head2.next.next.next = head1.next.next.next.next.next; // 8->6 System.out.println(getIntersectNode(head1, head2).value); } } ```

分层打印二叉树

思路

  • 主体思路用2个队列，根先入一个Q1，然后出对，按照顺序将左右孩子依次入到另外一个队列Q2
  • 遍历Q2的逻辑也是一样 出队之后，将其左右孩子依次入Q1
  • 一个Q一层，然后将另外一层入到另外一个队列即可
  • 注意空节点的打印 也要先获取树的最大层次
  • 大值打印效果如下
   1
 2   3
* * 4 5

代码

自己写的一个c++版本 ```c++ //定义二叉树节点 template struct Node{ T key;//数据元素 Node* left;//左孩子 Node* right;//右孩子 Node(T tIn){ key=tIn; left=right=nullptr; } }; //获取树的最大层次 //getMaxDepth 获取一个树的最大高度或者层次 根为第1层 template int getMaxDepth(Node* node) { if (node == nullptr) { return 0; } int depth = 1; depth += std::max(getMaxDepth(node->left), getMaxDepth(node->right)); return depth; } //分层打印二叉树 template void printByLevel(Node* root){ if (root ==nullptr){ return; } int depth = getMaxDepth(root) ; //获取树的最深层次 //申请2个队列 从1个队列出队 同时将其左右子树依次入队到另外一个队列 queue< Node* > q1,q2; queue< Node* > *cur=&q1,*next=&q2; q1.push(root); //终止条件 最大层次打印完毕 for (int i=1; i <= depth; ++i) { int count = 1 ; //标记打印当前层次的第几个元素 int tabCount = ( (1<<(depth+1-i)) - 1) / 2 ;//打印元素 计算打印前面\t个数 while( cur->empty()==false) { //队列1不为空 if (count > 1) { tabCount = ( (1<<(depth+1-i)) - 1); } Node* node=cur->front();cur->pop(); if (node != nullptr) { //不是空节点 //将其左右孩子入到下一层队列 for (int j = 0; j < tabCount; j++) { cout<<" "; } cout<key; count++; if (node->left != nullptr) { next->push(node->left); } else { next->push(nullptr); //加入一个空节点 为了打印好看 } if (node->right != nullptr) { next->push(node->right); } else { next->push(nullptr); //加入一个空节点 为了打印好看 } } else { //空节点 for (int j = 0; j < tabCount; j++) { cout<<" "; } cout<<"*"; count++; next->push(nullptr); //加入一个空节点 为了打印好看 next->push(nullptr); //加入一个空节点 为了打印好看 } } cout<* > *tmp=next;next=cur;cur=tmp;//交换队列指针指向 } } ```

如何判断一个树为完全二叉树

思路

准备一个队列,分层遍历，如果一个节点只有右孩子，没有左孩子 直接返回false，否则再判断这个节点是否左右孩子双全，如果不是，这个节点之后的所有节点都必须是叶子节点，否则为false，第一个遇到不是左右孩子双全的时候，将isCheckAllLeaf开关打开

  1. 根为空或者只有根返回true 否则根入队 isCheckAllLeaf初始化为false

  2. 队列为空则终止

  3. 从队列弹出一个节点，如果该节点只有右孩子，没有左孩子，直接返回false(不符合完全二叉树定义)，否则继续往下走

  4. 如果该节点不是左右孩子双全

    if ( isCheckAllLeaf){//如果开关已经打开 说明之前已经出现了孩子不全的情况了 之后出现的必须是叶子节点 所以直接返回false即可
	return false;
}else{
	isCheckAllLeaf=true;
}

  5. 循环完毕都没有返回false 那就return true

代码

转载java ```Java public static boolean isCBT(Node head) { if (head == null) { return true; } Queue queue = new LinkedList(); boolean leaf = false; Node l = null; Node r = null; queue.offer(head); while (!queue.isEmpty()) { head = queue.poll(); l = head.left; r = head.right; if ((leaf && (l != null || r != null)) || (l == null && r != null)) { return false; } if (l != null) { queue.offer(l); } if (r != null) { queue.offer(r); } else { leaf = true; } } return true; } ```

如何判断一个树为二叉搜索树 BST

思路

  1. 中序遍历 后面的树比前面的数要大即可
  2. 递归判断左右子树是否都是BST，同时得到左右子树的最大最小值，然后判断本节点是否BST(>左孩子最大值&&<右孩子最小值) 上面BST章节有go版本的代码

求完全二叉树个数

题目描述

已知一棵完全二叉树，求其节点的个数 要求:时间复杂度低于O(N)，N为这棵树的节点个数

思路

  • 肯定不能遍历 因为时间复杂度要低于O(N)
  • 利用完全二叉树的特点和满二叉树最大个数特点计算

大值逻辑如下：

​ 针对每一个节点都递归求解

  1. 先求树的最大高度(一路找左孩子 累计)

  2. 判断右子树最大高度跟其最大高度相等 如果相等则 其左孩子为满二叉树 个数为($2^(L-1)$ -1) L为最大高度 加上节点本身就是$2^L-1$，然后类似逻辑递归求接右子树的个数

  3. 如果右子树最大高度跟其最大高度不等 则其右孩子为满二叉树 假设右子树最大高度为LR 则右子树个数位$2^(LR-1)$ -1

    加上节点本身就是$2^(LR-1)$ ,然后递归求解左孩子的个数

代码

//递归伪代码
int getNodeNum(Node* root){
		int L=getMaxLevel(root);//该树最大高度
		int LR=getMaxLevel(root->right);//右子树最大高度
		int numLeft=0,numRight=0;//左子树个数 右子树个数
		if ( L==(LR+1)){
		//右子树最大高度跟其最大高度相等 如果相等则 其左孩子为满二叉树 个数为(2^(L-1) -1)  加上节点本身就是2^(L-1)
			numLeft=   ( 1<<(L-1) ) -1;
			return numLeft + 1 + getNodeNum(root->right); 
		}else{
		 //右子树最大高度跟其最大高度不等 则其右孩子为满二叉树 个数为 (2^(LR-1) -1) 
		 numRight= (  1<<(LR-1)  -1 );
		 return numRight + 1 + getNodeNum(root->left);
		}
}
转载Java实现 ```Java package class_04; public class Code_08_CompleteTreeNodeNumber { public static class Node { public int value; public Node left; public Node right; public Node(int data) { this.value = data; } } public static int nodeNum(Node head) { if (head == null) { return 0; } return bs(head, 1, mostLeftLevel(head, 1)); } public static int bs(Node node, int l, int h) { if (l == h) { return 1; } if (mostLeftLevel(node.right, l + 1) == h) { return (1 << (h - l)) + bs(node.right, l + 1, h); } else { return (1 << (h - l - 1)) + bs(node.left, l + 1, h); } } public static int mostLeftLevel(Node node, int level) { while (node != null) { level++; node = node.left; } return level - 1; } public static void main(String[] args) { Node head = new Node(1); head.left = new Node(2); head.right = new Node(3); head.left.left = new Node(4); head.left.right = new Node(5); head.right.left = new Node(6); System.out.println(nodeNum(head)); } } ```

折纸问题

题目描述

折纸问题 【题目】 请把一段纸条竖着放在桌子上，然后从纸条的下边向 上方对折1次，压出折痕后展开。此时 折痕是凹下去的，即折痕 突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折 2 次，压出折痕后展开，此时有三条折痕，从上到下依次是下折 痕、下折痕和上折痕。 给定一 个输入参数N，代表纸条都从下边向上方连续对折N次， 请从上到下打印所有折痕的方向。 例如:N=1时，打印: down N=2时，打印: down down up

思路

  • 要自己玩一下 转换为中序遍历

代码

转载 java ```Java public class Code_05_PaperFolding { public static void printAllFolds(int N) { printProcess(1, N, true); } public static void printProcess(int i, int N, boolean down) { if (i > N) { return; } printProcess(i + 1, N, true); System.out.println(down ? "down " : "up "); printProcess(i + 1, N, false); } public static void main(String[] args) { int N = 4; printAllFolds(N); } } ```

岛问题

题目描述

一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右 四个位置相连，如果有一片1连在一起，这个部分叫做一个岛，求一个 矩阵中有多少个岛?

举例:

001010

这个矩阵中有1个岛。

思路

  1. 遍历求解

    两层for循环遍历每一个点

    1 如果1个点是1 则将其改为2，同时将其上下左右是1的点也全都改为2(对于上下左右是1的点也要递归找到其上下左右是1的点改为2)，都改为2之后将岛的数量+1

    2 如果该点是2或者0 直接pass

    3 遍历结束返回岛累计计数结果

  2. 利用并查集结构。

    如果矩阵非常大，单机器单cpu则会比较慢，可以将矩阵分割为多个矩阵，利用多cpu或者多个机器并行计算，最后根据矩阵的边界，利用并查集结构求解，会提高效率。

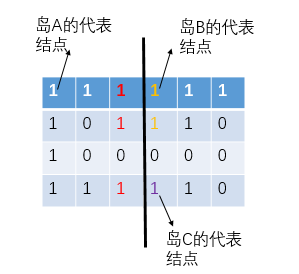
分析边界逻辑：

​ 1 如果2个点都是1，且对应的的代表节点不一样，则合并2个集合，岛数量减去1，否则跳过这对边界点 继续处理下一对边界点

​ 2 如果 一个是0 一个是1（说明2个岛无法连接 pass）

​ 3 如果 2个都是1，但是对应的代表节点一样(之前合并过了 本次直接跳过，岛数量不减)。

遍历求解代码

岛问题遍历递归求解 转载JAVA ```JAVA public class Code_03_Islands { public static int countIslands(int[][] m) { if (m == null || m[0] == null) { return 0; } int N = m.length; int M = m[0].length; int res = 0; for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { if (m[i][j] == 1) { res++; infect(m, i, j, N, M); } } } return res; } public static void infect(int[][] m, int i, int j, int N, int M) { if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) { return; } m[i][j] = 2; infect(m, i + 1, j, N, M); infect(m, i - 1, j, N, M); infect(m, i, j + 1, N, M); infect(m, i, j - 1, N, M); } public static void main(String[] args) { int[][] m1 = { { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 1, 1, 1, 0, 1, 1, 1, 0 }, { 0, 1, 1, 1, 0, 0, 0, 1, 0 }, { 0, 1, 1, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, { 0, 0, 0, 0, 1, 1, 1, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, }; System.out.println(countIslands(m1)); int[][] m2 = { { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 1, 1, 1, 1, 1, 1, 1, 0 }, { 0, 1, 1, 1, 0, 0, 0, 1, 0 }, { 0, 1, 1, 0, 0, 0, 1, 1, 0 }, { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, { 0, 0, 0, 0, 1, 1, 1, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, }; System.out.println(countIslands(m2)); } } ```

拼接最小字典序

题目描述

给定一个字符串类型的数组strs，找到一种拼接方式，使得把所有字符串拼起来之后形成的字符串具有最低的字典序

不能直接按照字典序排序数组，然后拼接因为假设有 “b” “ba” 这就是字典序排序后的东西 拼接出来的bba 不如bab

也就是比较器需要自己实现

str1+str2<=str2+str1 返回str1 否则返回str2

//转载 JAVA
public static class MyComparator implements Comparator<String> {
		@Override
		public int compare(String a, String b) {
			return (a + b).compareTo(b + a);
		}
	}
	public static String lowestString(String[] strs) {
		if (strs == null || strs.length == 0) {
			return "";
		}
		// 用自己定义的比较器搞 c/c++就是重载比较运算符
		Arrays.sort(strs, new MyComparator());
		String res = "";
		for (int i = 0; i < strs.length; i++) {
			res += strs[i];
		}
		return res;
	}

分金条代价最小

题目描述

一块金条切成两半，是需要花费和长度数值一样的铜板的。比如 长度为20的 金条，不管切成长度多大的两半，都要花费20个铜 板。

一群人想整分整块金条，怎么分最省铜板? 例如,给定数组{10,20,30}，代表一共三个人，整块金条长度为 10+20+30=60. 金条要分成10,20,30三个部分。

如果， 先把长 度60的金条分成10和50，花费60 再把长度50的金条分成20和30， 花费50 一共花费110铜板。

如果， 先把长度60的金条分成30和30，花费60 再把长度30 金条分成10和20，花费30 一共花费90铜板。 输入一个数组，返回分割的最小代价。

思路

​ 这个其实就是哈夫曼编码问题，也是典型的贪心问题，策略就是找2个最小元素相加，这个和就是分割的花费，然后再将这个最小和作为新的元素 放进集合，再从中挑选2个最小的数相加累计花费，最后只剩下一个元素结束。

可以用最小堆实现，先将数组元素全部入堆，先后弹出2个元素(当前数组中最小的)，花费+=弹出的2元素之和，同时再将元素和入堆 知道最后堆只剩下一个元素。

代码

//转载 JAVA
//PriorityQueue是Java语言对堆结构的一个实现，默认将按自然顺序的最小元素放在堆顶
  PriorityQueue<Integer> minHeap = new PriorityQueue();
  for (int i : arr) {
    minHeap.add(i);
  }
  int res = 0;
  int curCost = 0;
  while (minHeap.size() > 1) {
    curCost = minHeap.poll() + minHeap.poll();
    res += curCost;
    minHeap.add(curCost);
  }
  return res

IPO问题

题目描述:

定若干个项目。对于每个项目 i，它都有一个纯利润 Pi，并且需要最小的资本 Ci 来启动相应的项目。最初，你有 W 资本。当你完成一个项目时，你将获得纯利润，且利润将被添加到你的总资本中。

总而言之，从给定项目中选择最多 k 个不同项目的列表，以最大化最终资本，并输出最终可获得的最多资本。

示例 1:

输入: k=2, W=0, Profits=[1,2,3], Capital=[0,1,1].

输出: 4

解释: 由于你的初始资本为 0，你尽可以从 0 号项目开始。 在完成后，你将获得 1 的利润，你的总资本将变为 1。 此时你可以选择开始 1 号或 2 号项目。 由于你最多可以选择两个项目，所以你需要完成 2 号项目以获得最大的资本。 因此，输出最后最大化的资本，为 0 + 1 + 3 = 4。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/ipo

思路：

​ 也是贪心 贪心一般都有堆实现，准备2个堆1个大根堆(按照项目利润排序)，一个小根堆(按照项目成本排序)

  1. 首先对应Captial成本数组 一个入小根堆(成本最低的在堆顶)

  2. 循环将堆顶的项目成本Ci<=W的所有项目 对应的利润扔到大根堆 ，所以目前大根堆里面的项目都是解锁的项目，也就是手里有钱可以做的，如果大根堆size为0，代表没有可以做的项目 直接返回即可，已完成项目次数到达了K 也直接返回即可 否则继续下面逻辑

    然后弹出大根堆的堆顶，可以做的项目中挑选一个最大的，然后W+=Pi 手里的钱要加上利润，K++,然后循环步骤2

代码

IPO问题代码 转载JAVA ```Java public class Code_03_IPO { public static class Node { public int p; public int c; public Node(int p, int c) { this.p = p; this.c = c; } } public static class MinCostComparator implements Comparator { @Override public int compare(Node o1, Node o2) { return o1.c - o2.c; } } public static class MaxProfitComparator implements Comparator { @Override public int compare(Node o1, Node o2) { return o2.p - o1.p; } } public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) { Node[] nodes = new Node[Profits.length]; for (int i = 0; i < Profits.length; i++) { nodes[i] = new Node(Profits[i], Capital[i]); } PriorityQueue minCostQ = new PriorityQueue<>(new MinCostComparator()); PriorityQueue maxProfitQ = new PriorityQueue<>(new MaxProfitComparator()); for (int i = 0; i < nodes.length; i++) { minCostQ.add(nodes[i]); } for (int i = 0; i < k; i++) { while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) { maxProfitQ.add(minCostQ.poll()); } if (maxProfitQ.isEmpty()) { return W; } W += maxProfitQ.poll().p; } return W; } } ```

会议室宣讲安排问题

题目定义

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目 的宣讲。

给你每一个项目开始的时间和结束的时间(给你一个数组，里面是一个个具体的项目)，你来安排宣讲的日程，

要求会议室进行 的宣讲的场次最多。返回这个最多的宣讲场次。

思路

  1. 贪心1 次数最多，谁的会议时间开始越早谁先安排

    可以举出反例子，如果最早开始的项目 占用全天时间，别的会议都不能安排了

  2. 会议持续时间越短 就安排

    也不行，也可以举出反例 A会议[6–>12] B会议[11:30–>14:00] C会议[13:30—>20] 如果安排了B会议。A会议和C会议都不能安排了

  3. 这道题正确的贪心是谁的结束时间越早 越先安排

    谁的结束时间越早，就安排，然后淘汰因为安排了这个会议不能安排的会议，然后继续挑选结束时间最早的安排(淘汰相关不能安排的)

代码

转载Java ```Java public class Schedule { public class Project { int start; int end; } public class MostEarlyEndComparator implements Comparator { public int compare(Project p1, Project p2) { return p1.end-p2.end; } } public int solution(Project projects[],int currentTime) { //sort by the end time Arrays.sort(projects, new MostEarlyEndComparator()); int res = 0; for (int i = 0; i < projects.length; i++) { if (currentTime <= projects[i].start) { res++; currentTime = projects[i].end; } } return res; } } ```

打印一个字符串的所有子序列

  • 子序列跟字串有区别 字串必须是连续的，子序列不是，但不能改变顺序
  • 比如 abc 是 “abcdef”的字串 也是子序列 adf是 “abcedf”的子序列 但不是子串。bac不是"abcedf"的子序列 也不是子串

思路

递归

顺序遍历字符串每一个字符，针对每一个字符都只有2种情况，要或者不要

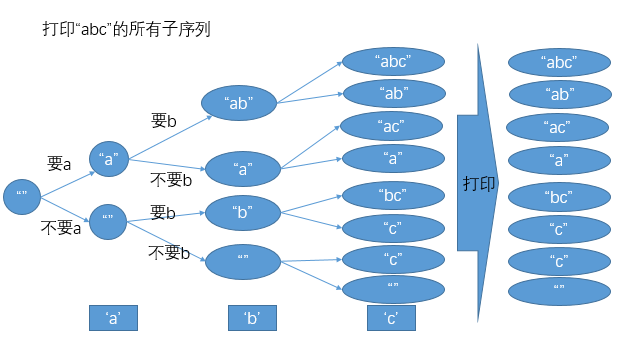
代码
//begin为从第几个索引位置开始 res为到这个索引已经得到的子序列
void printAllSub(string& str,int begin,string res){
    if(begin >=str.length()){//如果全部遍历完成 直接打印即可
        cout<<res<<endl;
        return;
    }
    printAllSub(str,begin+1,res);//不要begin位置的字符
    printAllSub(str,begin+1,res+str[begin]);
}
int main(){
	string str="abc";
    printAllSub(str,0,"");
}

打印字符串的全排列

这种就可以打乱顺序了，但是必须每个字符都要，而且不能重复。

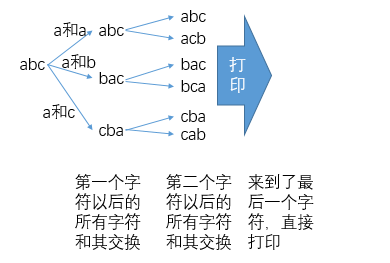
public static void printAllPermutations(char[] chs,int index) {
  //base case
  if(index == chs.length-1) {
    System.out.println(chs);
    return;
  }
  for (int j = index; j < chs.length; j++) {
    swap(chs,index,j);
    printAllPermutations(chs, index+1);
  }
}

母牛生牛问题

母牛每年生一只母牛，新出生的母牛成长三年后也能每年生一只母牛，假设不会死。求N年后，母牛的数量。

先画出简单的前面几项 看是否能找到规律

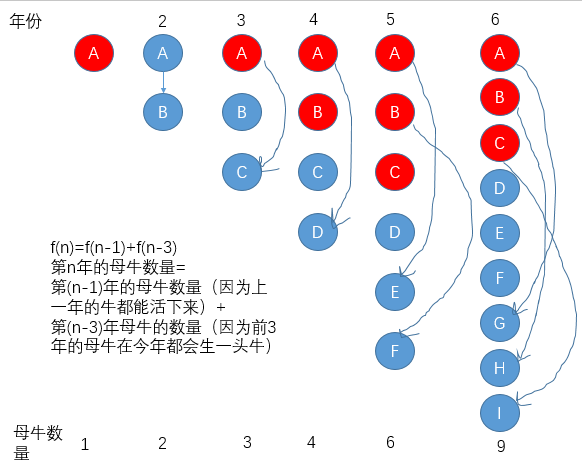
public static int cowNumber(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2 || n == 3) {
			return n;
		}
		return cowNumber(n - 1) + cowNumber(n - 3);
	}

递归逆序栈

public static void reverse(Stack<Integer> stack) {
		if (stack.isEmpty()) {
			return;
		}
		int i = getAndRemoveLastElement(stack);//得到当前栈最后一个元素(栈底元素 最先入栈的元素) 并且从栈种移除  其它元素不动
		reverse(stack);//得到剩余栈最后一个元素 并且从栈种移除 其它元素不动
		//如果入栈是1 2 3 那么i顺序得到 3 2 1
		stack.push(i);//然后按照顺序入栈3 2 1 就相当于完成了逆序这个栈
	}
	public static int getAndRemoveLastElement(Stack<Integer> stack) {
		int result = stack.pop();//持续得到栈顶元素 得到顺序为3 2 1
		if (stack.isEmpty()) {//栈为空则 直接返回 
			return result;
		} else { 
			int last = getAndRemoveLastElement(stack);//不为空 则继续递归弹出栈顶 最后得到1 栈底元素
			stack.push(result); 
			return last;
			//除了最后一个元素 将依次出栈的元素 按照相关的顺序继续入栈(除了栈底元素出栈外 其它不变) 同时一直返回栈底元素
		}
	}

链表中倒数第K个节点

题目描述

输入一个链表，输出该链表中倒数第k个结点。

整体思路：

  1. 假象有一个节点tmp 它的下一个节点指向第一个节点head。 p1,p2都指向tmp
  2. p1先往前走k步
  3. 然后p1 p2都逐步往前走，当p1==null 此时p2就是倒数第k个节点(因为p1先走了k步)
public ListNode FindKthToTail(ListNode head,int k) {
    //input check
    if(head == null || k <= 0){
        return null;
    }
    ListNode tmp = new ListNode(0);
    tmp.next = head;
    ListNode p1 = tmp, p2 = tmp;
    while(k > 0 && p1.next != null){
        p1 = p1.next;
        k--;
    }
    //length < k
    if(k != 0){
        return null;
    }
    while(p1 != null){
        p1 = p1.next;
        p2 = p2.next;
    }
    
    tmp = null; //help gc

    return p2;
}

合并2个排序链表

题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则

思路

利用归并排序的合并步骤 完成次操作

代码

public ListNode Merge(ListNode list1,ListNode list2) {
    if(list1 == null || list2 == null){
        return list1 == null ? list2 : list1;
    }
    ListNode newHead = list1.val < list2.val ? list1 : list2;
    ListNode p1 = (newHead == list1) ? list1.next : list1;
    ListNode p2 = (newHead == list2) ? list2.next : list2;
    ListNode p = newHead;
    while(p1 != null && p2 != null){
        if(p1.val <= p2.val){
            p.next = p1;
            p1 = p1.next;
        }else{
            p.next = p2;
            p2 = p2.next;
        }
        p = p.next;
    }
    while(p1 != null){
        p.next = p1;
        p = p.next;
        p1 = p1.next;
    }
    while(p2 != null){
        p.next = p2;
        p = p.next;
        p2 = p2.next;
    }
    return newHead;
}

判断是否为树的子结构

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

思路：

树的很多解法都是递归，这道题也是如此。递归判断头节点 左子树 右子树 。大值分为2种情况

  1. 如果root1.val==root2.val 并且root2.left也是root1.left的子结构(递归) 并且root2.right也是root1.right的子结构(递归)
  2. 否则 就要看 root2是否为root1.left的子结构(递归) 或者root1.right的子结构(递归)

难点是base-case,也就是递归终止的条件

  • 子过程root2=null那么说明在自上而下的比较过程中root2的结点已被罗列比较完了，这时无论root1是否为null，该子过程都应该返回true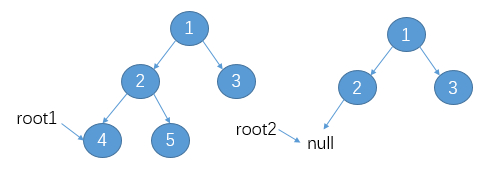

  • root2 != null`而`root1 = null`，则应返回`false

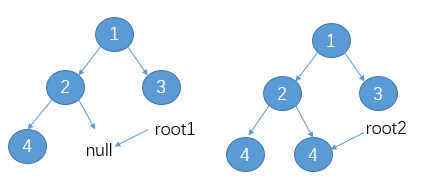
代码

public class Solution {
    public boolean HasSubtree(TreeNode root1,TreeNode root2) {
        if(root1 == null || root2 == null){
            return false;
        }

        return process(root1, root2);
    }
    public boolean process(TreeNode root1, TreeNode root2){
        if(root2 == null){
            return true;
        }
        if(root1 == null && root2 != null){
            return false;
        }  

        if(root1.val == root2.val){
            if(process(root1.left, root2.left) && process(root1.right, root2.right)){
                return true;
            }
        }
        return process(root1.left, root2) || process(root1.right, root2);
    }
}

二叉树镜像

题目描述

操作给定的二叉树，将其变换为源二叉树的镜像。

思路：

​ 仔细看图，对于每个节点交换左右孩子 递归交换 注意base-case那就是节点已经到空节点了 那就return

代码

public void Mirror(TreeNode root) {
    if(root == null){
        return;
    }
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;
    Mirror(root.left);
    Mirror(root.right);
}

栈的压入、弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

思路

要冷静分析找规律

可以使用两个指针i,j，初始时i指向压入序列的第一个，j指向弹出序列的第一个，试图将压入序列按照顺序压入栈中：

  1. 如果arr1[i] != arr2[j]，那么将arr1[i]压入栈中并后移i（表示arr1[i]还没到该它弹出的时刻）
  2. 如果某次后移i之后发现arr1[i] == arr2[j]，那么说明此刻的arr1[i]被压入后应该被立即弹出才会产生给定的弹出序列，于是不压入arr1[i]（表示压入并弹出了）并后移i，j也要后移（表示弹出序列的arr2[j]记录已产生，接着产生或许的弹出记录即可）。
  3. 因为步骤2和3都会后移i，因此循环的终止条件是i到达arr1.length，此时若栈中还有元素，那么从栈顶到栈底形成的序列必须与arr2中j之后的序列相同才能返回true。

代码

public boolean IsPopOrder(int [] arr1,int [] arr2) {
    //input check
    if(arr1 == null || arr2 == null || arr1.length != arr2.length || arr1.length == 0){
        return false;
    }
    Stack<Integer> stack = new Stack();
    int length = arr1.length;
    int i = 0, j = 0;
    while(i < length && j < length){
        if(arr1[i] != arr2[j]){
            stack.push(arr1[i++]);
        }else{
            i++;
            j++;
        }
    }
    while(j < length){
        if(arr2[j] != stack.peek()){
            return false;
        }else{
            stack.pop();
            j++;
        }
    }
    return stack.empty() && j == length;
}

二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

 5
/ \

2 6 /
1 3 示例 1：

输入: [1,6,3,2,5] 输出: false 示例 2：

输入: [1,3,2,6,5] 输出: true

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof

思路

post的遍历顺序为“左右根”，每一层判断左右子树和根节点的大小关系，如果满足则继续向下判断；否则直接返回失败 具体做法是： （1）遍历本层数组，找到比根节点(即数组最后一个数)大的第一个节点，此节点向左都是左子树，此节点向右都是右子树 （2）上一步已经把左子树的合法性证实了，只需要证实右子树的合法性，即判断右子树所有值大于根节点。右子树合法则继续下一层判断，否则直接返回false

作者：yyc-13 链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/solution/jian-zhi-offer-33-er-cha-sou-suo-shu-de-hou-xu-b-4/

代码

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        if(postorder.size()<=1){
            return true;
        }
        return Recur(postorder,0,postorder.size()-1);
    }
    bool Recur(vector<int>& postorder,int i,int j){
        if(i>=j){
            return true;
        }
        int m;
        for(m=0;m<j;m++){
            if(postorder[m]>postorder[j]){
                break;
            }
        }
        for(int k=m+1;k<j;k++){
            if(postorder[k]<postorder[j]){
                return false;
            }
        }
        return Recur(postorder,i,m-1)&&Recur(postorder,m,j-1);
    }
};

二叉树中和为某一值的路径

题目描述

输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

整体思路：

  1. 首先我们要从上到下 从根节点到每个叶子节点的遍历 这就是先序遍历，另外遍历的时候需要将结果累计起来 ，同时也要把路过的节点给记录下来(可以用到栈)

代码

public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
    ArrayList<ArrayList<Integer>> res = new ArrayList();
    if(root == null){
        return res;
    }
    Stack<Integer> stack = new Stack<Integer>();
    preOrder(root, stack, 0, target, res);
    return res;
}
public void preOrder(TreeNode root, Stack<Integer> stack, int sum, int target, 
                     ArrayList<ArrayList<Integer>> res){
    if(root == null){
        return;
    }
    stack.push(root.val);
    sum += root.val;
    //leaf node
    if(root.left == null && root.right == null && sum == target){
        ArrayList<Integer> one = new ArrayList();
        one.addAll(stack);
        res.add(one);
    }
    preOrder(root.left, stack, sum, target, res);
    preOrder(root.right, stack, sum, target, res);
    sum -= stack.pop();
}

BST转排序双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

整体思路：

一、搜索二叉树的特点：

（1）其左子树的结点均小于它，其右子树的结点均大于它； （2）其子树也是搜索二叉树； 根据二叉树 特点（2） 可联想到使用递归；

二、问题分解如下：

设：有任意结点 r step 1 将r的左子树变为有序链表，要输出此有序链表的头尾结点 Lhead、LTail； step 2 将r的右子树变为有序链表，要输出此有序链表的头尾结点 Rhead、RTail； step 3 将r结点与左有序链表和右有序两边连接；即将Ltail结点与r->left连接；将r->right 与 Rhead与其连接； step 4 返回以r结点为根的树的头与尾 ：Lhead、RTail 截止条件：r 为叶子结点

作者：JameyGo 链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/solution/di-gui-yi-li-jie-by-jameygo/

代码

class Solution {
public:
	Node* treeToDoublyList(Node* root) {
		if (root == NULL){//如果树为空 则直接返回
			return NULL;
		}
		Node* head, *tail;
		//找到其双向链表的头尾节点 
		listTree(root, head, tail);
		head->left = tail;//头的前驱指向尾节点
		tail->right = head;//尾的后继指向头节点
		return head;//返回头节点
	}
	//针对每个节点将其看成单独的树 找到其双向链表的头节点和尾节点
	void listTree(Node* r, Node* &head, Node* &tail){
		if (r == NULL){//如果达到叶子节点 则直接返回
			return;
		}
		Node* lhead, *ltail,*rhead,*rtail;//分别是左子树链表的头节点和尾节点 右子树的头节点和尾部节点
		lhead = r;//左子树链表的头节点先指向当前节点
		if (r->left!=NULL){//如果有左孩子 递归调用listTree找到左子树链表的头尾节点
			listTree(r->left, lhead, ltail);
			r->left = ltail;//当前节点的前驱指向左子树链表 尾节点
			ltail->right = r;//左子树链表 尾节点的后继指向当前节点
		}
		rtail = r;//右子树链表的尾部节点也先指向当前节点
		if (r->right != NULL){//如果有右孩子 递归调用listTree找到右子树链表的头尾节点
			listTree(r->right, rhead, rtail);
			r->right = rhead;//当前节点后继节点指向右子树链表的头节点
			rhead->left = r;//右子树链表的头节点的前驱指向当前节点
		}
		head = lhead;//左子树右子树都处理完毕 整个链表的头节点就是左子树链表的头节点
		tail = rtail;//整个链表的尾节点就是右子树链表的尾节点
	}
};